2021年浙教版数学八年级上册《三角形的初步知识》期末复习卷（含答案）

2021年浙教版数学八年级上册

《三角形的初步知识》期末复习卷

一、选择题

1.下列语句中，不是命题的是(    )

A.若两角之和为90°，则这两个角互补

B.同角的余角相等

C.作线段的垂直平分线

D.相等的角是对顶角

2.下列命题中，正确的命题是(   )

A.3是9的算术平方根

B.9的平方根是3

C.的算术平方根是4

D.内错角相等

3.若长度分别为2，7，x的三条线段能组成一个三角形，则x的值可以是(     )

A.4　　　 B.5　　　 C.6　　　 D.9

4.如图，在△ABC中，点D在AB上，点E在AC上，DE∥BC．若∠A=62°，∠AED=54°，

则∠B的度数为(    )

A.54°        B.62°      C.64°        D.74°

5.在下列各图形中，分别画出了△ABC中BC边上的高AD，其中正确的是（    ）

  A.      B.    C.      D.

6.如图，两个三角形是全等三角形，那么x的值是(　　)

A.30°         B.45°         C.50°         D.85°

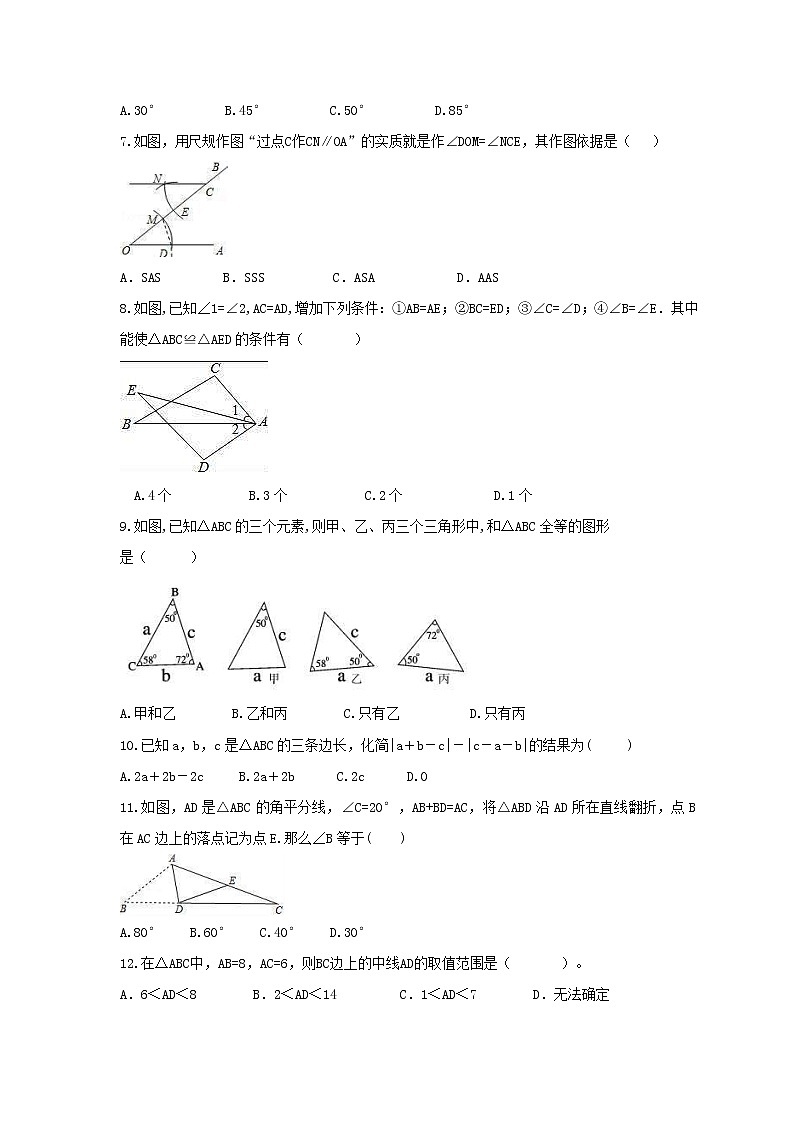
7.如图，用尺规作图“过点 C 作 CN∥OA”的实质就是作∠DOM=∠NCE，其作图依据是（                 ）

A．SAS                       B．SSS                        C．ASA                          D．AAS

8.如图,已知∠1=∠2,AC=AD,增加下列条件：①AB=AE；②BC=ED；③∠C=∠D；④∠B=∠E．其中能使△ABC≌△AED的条件有（       ）

  A.4个                         B.3个                         C.2个                           D.1个

9.如图,已知△ABC的三个元素,则甲、乙、丙三个三角形中,和△ABC全等的图形

是（      ）

A.甲和乙        B.乙和丙        C.只有乙          D.只有丙

10.已知a，b，c是△ABC的三条边长，化简|a＋b－c|－|c－a－b|的结果为(     )

A.2a＋2b－2c     B.2a＋2b      C.2c      D.0

11.如图，AD是△ABC的角平分线，∠C=20°，AB+BD=AC，将△ABD沿AD所在直线翻折，点B在AC边上的落点记为点E.那么∠B等于(　　)

A.80°    B.60°    C.40°    D.30°

12.在△ABC中，AB=8，AC=6，则BC边上的中线AD的取值范围是（       ）。

A．6＜AD＜8        B．2＜AD＜14         C．1＜AD＜7        D．无法确定

二、填空题

13.命题“对顶角相等”的“条件”是　　　　　　            .

14.一个三角形3条边长分别为x cm、(x+1)cm、(x+2)cm,它的周长不超过39 cm,则x的取值范围是　　　　.

15.如图，已知△OAB≌△OCD，∠A=30°，∠AOB=105°，则∠D=　   　°.

16.如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是　    　.

17.如图，点B，C，E，F在一直线上，AB∥DC，DE∥GF，∠B=∠F=72°，则∠D=     度.

18.如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H.

下面说法中正确的序号是　    .

①△ABE的面积等于△BCE的面积；

②∠AFG=∠AGF；

③∠FAG=2∠ACF；④BH=CH.

三、作图题

19.如图，已知线段a，b及∠α．求作：△ABC，使其有一个内角等于∠α，且∠α的对边等于a，另一边等于b(要求：尺规作图，保留作图痕迹)．

四、解答题

20.如图，已知△ABC的周长为21cm，AB=6cm，BC边上中线AD=5cm，△ABD周长为15cm，求AC长.

21.如图，在△ABC中，AD是高线，AE，BF是角平分线，它们相交于点O，∠CAB=50°，

∠C=60°，求∠DAE和∠BOA的度数．

22.如图，已知AB=AE，∠1=∠2，∠B=∠E．求证：BC=ED．

23.某风景区改建中，需测量湖两岸游船码头A、B间的距离，于是工作人员在岸边A、B的垂线AF上取两点E、D，使ED=AE.再过D点作出AF的垂线OD，并在OD上找一点C，使B、E、C在同一直线上，这时测得CD长就是AB的距离.请说明理由.

24.如图，Rt△ABC中，∠ACB=90°，AC=BC，点D在斜边AB上，且AD=AC，过点B作BE⊥CD交直线CD于点E.

(1)求∠BCD的度数；

(2)作AF⊥CD于点F，求证：△AFD≌△CEB.

(3)请直接写出CD与BE的数量关系(不需证明).

25.已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,

CE⊥AE于E.

 (1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由；

 (2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何？请说明理由；

 (3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.

参考答案

1.答案为：C.

2.答案为：A.

3.答案为：C.

4.答案为：C.

5.答案为：B

6.答案为：C.

7.答案为：B.

8.答案为：B

9.答案为：B

10.答案为：D.

11.答案为：C.

12.答案为：C

13.答案为：两个角是对顶角.

14.答案为：1<x≤12

15.答案为：45.

16.答案为：乙、丙.

17.答案为：36°

18.答案为：①②③.

19.解：作法如下：

(1)作∠MBN=∠α．

(2)在BM上截取线段AB=b．

(3)以点A为圆心，a为半径画弧，交BN于点C1，C2，连结AC1，AC2，

则△ABC1和△ABC2即为所求作的三角形(如图)．

20.答案为：7

21.解：∵∠CAB=50°，∠C=60°，

∴∠ABC=180°－50°－60°=70°．

∵AD是高线，∴∠ADC=90°，

∴∠DAC=180°－∠ADC－∠C=30°．

∵AE，BF是角平分线，

∴∠ABF=∠ABC=35°，∠EAF=∠CAB=25°，

∴∠DAE=∠DAC－∠EAF=5°，

∠AFB=180°－∠ABF－∠CAB=95°，

∴∠AOF=180°－∠AFB－∠EAF=60°，

∴∠BOA=180°－∠AOF=120°．

22.证明：∵∠1=∠2，

∴∠1+∠BAD=∠2+∠BAD，

即：∠EAD=∠BAC，

在△EAD和△BAC中

，

∴△ABC≌△AED（ASA），

∴BC=ED．

23.证明：∵AB⊥AD，CD⊥AD

∴∠A=∠CDE=90°

又∵ED=AE，∠AEB=∠CED

∴△ABE≌△CED(AAS)

所以AB=CD.

24.解：(1)∵∠ACB=90°，AC=BC，

∴∠A=∠B=45°，

∵AD=AC，

∴∠ACD=∠ADC==67.5°，

∴∠BCD=90°﹣67.5°=22.5°；

(2)∵AD=AC，

∴CF=FD=CD，∠FAD=CAB=22.5°，

∵∠ADC=67.5°，

∴∠BDE=67.5°，

∴∠DBE=22.5°，

∴∠CBE=67.5°，

在△AFD和△CEB中，

，

∴△AFD≌△CEB，

(3)CD=2BE，理由如下；

∵△AFD≌△CEB，

∴BE=DF，

∴CD=2BE.

25.解：（1）在△ABC中,∠BAC=90°，

∴∠BAD＝90°-∠EAC。

又∵BD⊥AE于D，CE⊥AE于E，

∴∠BAD＝90°-∠EAC=∠ACE。

而AB=AC，

于是△ABD全等于△CAE，BD=AE,AD=CE。

因此，BD=AE=AD+DE=DE+CE。

（2）DE=BD+CE。

理由：与（1）同理，可得△ABD全等于△CAE，

于是BD=AE,CE=AD，DE=AE+AD=BD+CE。

（3）当直线AE与线段BC有交点时，BD=DE+CE；

当直线AE交于线段BC的延长线上时，DE=BD+CE。