

2019年人教版四川省乐山市中考数学试卷及答案解析
展开2019年四川省乐山市中考数学试卷
一、选择题:本大题共10个小题,每小题3分,共30分.
1.(3分)﹣3的绝对值是( )
A.3 B.﹣3 C. D.
2.(3分)下列四个图形中,可以由图通过平移得到的是( )
A. B. C. D.
3.(3分)小强同学从﹣1,0,1,2,3,4这六个数中任选一个数,满足不等式x+1<2的概率是( )
A. B. C. D.
4.(3分)﹣a一定是( )
A.正数 B.负数
C.0 D.以上选项都不正确
5.(3分)如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,那么∠2等于( )
A.45° B.50° C.55° D.60°
6.(3分)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
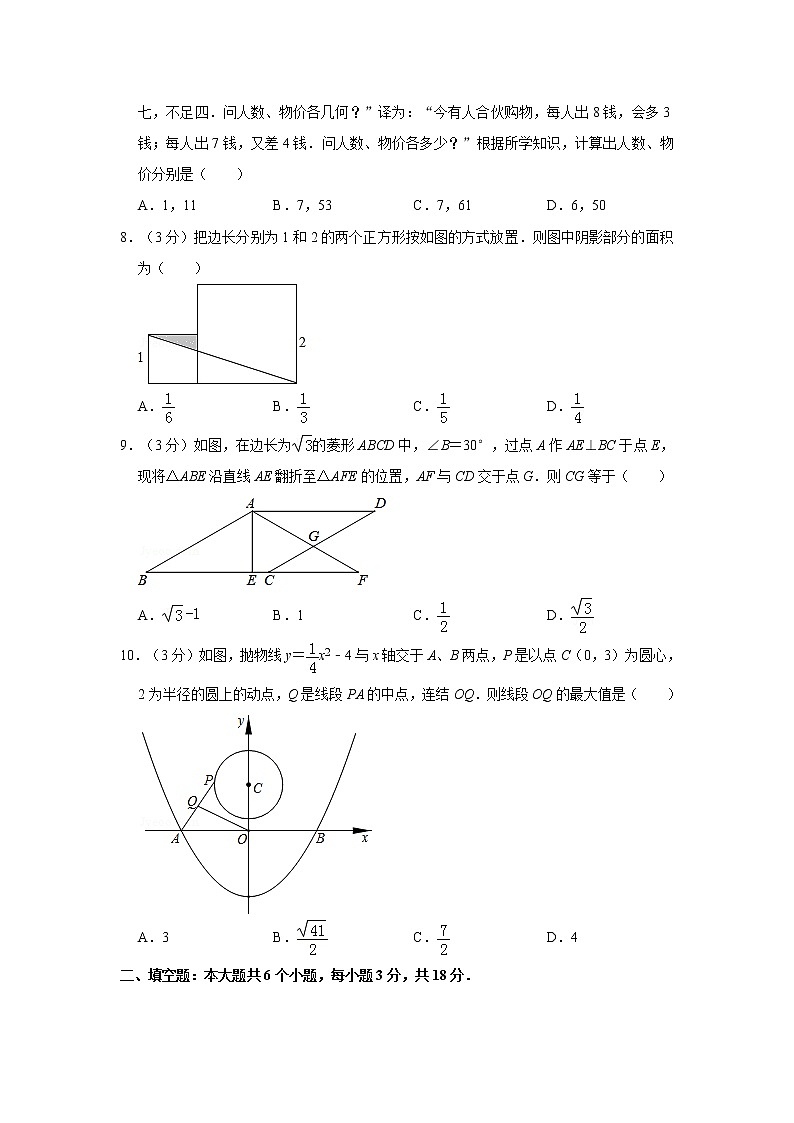
7.(3分)《九章算术》第七卷“盈不足”中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少?”根据所学知识,计算出人数、物价分别是( )
A.1,11 B.7,53 C.7,61 D.6,50
8.(3分)把边长分别为1和2的两个正方形按如图的方式放置.则图中阴影部分的面积为( )
A. B. C. D.
9.(3分)如图,在边长为的菱形ABCD中,∠B=30°,过点A作AE⊥BC于点E,现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G.则CG等于( )
A. B.1 C. D.
10.(3分)如图,抛物线y=x2﹣4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是( )
A.3 B. C. D.4
二、填空题:本大题共6个小题,每小题3分,共18分.
11.(3分)﹣的相反数是 .
12.(3分)某地某天早晨的气温是﹣2℃,到中午升高了6℃,晚上又降低了7℃.那么晚上的温度是 ℃.
13.(3分)若3m=9n=2.则3m+2n= .
14.(3分)如图,在△ABC中,∠B=30°,AC=2,cosC=.则AB边的长为 .
15.(3分)如图,点P是双曲线C:y=(x>0)上的一点,过点P作x轴的垂线交直线AB:y=x﹣2于点Q,连结OP,OQ.当点P在曲线C上运动,且点P在Q的上方时,△POQ面积的最大值是 .
16.(3分)如图1,在四边形ABCD中,AD∥BC,∠B=30°,直线l⊥AB.当直线l沿射线BC方向,从点B开始向右平移时,直线l与四边形ABCD的边分别相交于点E、F.设直线l向右平移的距离为x,线段EF的长为y,且y与x的函数关系如图2所示,则四边形ABCD的周长是 .
三、本大题共3个小题,每小题9分,共27分.
17.(9分)计算:()﹣1﹣(2019﹣π)0+2sin30°.
18.(9分)如图,点A、B在数轴上,它们对应的数分别为﹣2,,且点A、B到原点的距离相等.求x的值.
19.(9分)如图,线段AC、BD相交于点E,AE=DE,BE=CE.求证:∠B=∠C.
四、本大题共3个小题,每小题10分,共30分.
20.(10分)化简:÷.
21.(10分)如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(﹣1,a).
(1)求直线l1的解析式;
(2)求四边形PAOC的面积.
22.(10分)某校组织学生参加“安全知识竞赛”,测试结束后,张老师从七年级720名学生中随机地抽取部分学生的成绩绘制了条形统计图,如图所示.试根据统计图提供的信息,回答下列问题:
(1)张老师抽取的这部分学生中,共有 名男生, 名女生;
(2)张老师抽取的这部分学生中,女生成绩的众数是 ;
(3)若将不低于27分的成绩定为优秀,请估计七年级720名学生中成绩为优秀的学生人数大约是多少.
五、本大题共2个小题,每小题10分,共20分.
23.(10分)已知关于x的一元二次方程x2﹣(k+4)x+4k=0.
(1)求证:无论k为任何实数,此方程总有两个实数根;
(2)若方程的两个实数根为x1、x2,满足+=,求k的值;
(3)若Rt△ABC的斜边为5,另外两条边的长恰好是方程的两个根x1、x2,求Rt△ABC的内切圆半径.
24.(10分)如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连结CP并延长交⊙O于另一点B,且AB=AC.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为3,求线段BP的长.
六、本大题共2个小题,第25题12分,第26题13分,共25分.
25.(12分)在△ABC中,已知D是BC边的中点,G是△ABC的重心,过G点的直线分别交AB、AC于点E、F.
(1)如图1,当EF∥BC时,求证:+=1;
(2)如图2,当EF和BC不平行,且点E、F分别在线段AB、AC上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
(3)如图3,当点E在AB的延长线上或点F在AC的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
26.(13分)如图,已知抛物线y=a(x+2)(x﹣6)与x轴相交于A、B两点,与y轴交于C点,且tan∠CAB=.设抛物线的顶点为M,对称轴交x轴于点N.
(1)求抛物线的解析式;
(2)P为抛物线的对称轴上一点,Q(n,0)为x轴上一点,且PQ⊥PC.
①当点P在线段MN(含端点)上运动时,求n的变化范围;
②当n取最大值时,求点P到线段CQ的距离;
③当n取最大值时,将线段CQ向上平移t个单位长度,使得线段CQ与抛物线有两个交点,求t的取值范围.
2019年四川省乐山市中考数学试卷
参考答案与试题解析
一、选择题:本大题共10个小题,每小题3分,共30分.
1.解:|﹣3|=﹣(﹣3)=3.
故选:A.
2.解:∵只有D的图形的形状和大小没有变化,符合平移的性质,属于平移得到;
故选:D.
3.解:在﹣1,0,1,2,3,4这六个数中,满足不等式x+1<2的有﹣1、0这两个,
所以满足不等式x+1<2的概率是=,
故选:C.
4.解:﹣a中a的符号无法确定,故﹣a的符号无法确定.
故选:D.
5.解:∵a∥b,∠1=35°,
∴∠BAC=∠1=35°.
∵AB⊥BC,
∴∠2=∠BCA=90°﹣∠BAC=55°.
故选:C.
6.解:,
解①得:x>﹣6,
解②得:x≤13,
故不等式组的解集为:﹣6<x≤13,
在数轴上表示为:.
故选:B.
7.解:设有x人,物价为y,可得:,
解得:,
故选:B.
8.解:
如图,设BC=x,则CE=1﹣x
易证△ABC∽△FEC
∴===
解得x=
∴阴影部分面积为:S△ABC=××1=
故选:A.
9.解:在Rt△ABE中,∠B=30°,AB=,
∴BE=.
根据折叠性质可得BF=2BE=3.
∴CF=3﹣.
∵AD∥CF,
∴△ADG∽△FCG.
∴.
设CG=x,则,
解得x=﹣1.
故选:A.
10.解:连接BP,如图,
当y=0时,x2﹣4=0,解得x1=4,x2=﹣4,则A(﹣4,0),B(4,0),
∵Q是线段PA的中点,
∴OQ为△ABP的中位线,
∴OQ=BP,
当BP最大时,OQ最大,
而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,
∵BC==5,
∴BP′=5+2=7,
∴线段OQ的最大值是.
故选:C.
二、填空题:本大题共6个小题,每小题3分,共18分.
11.解:的相反数是,
故答案为:.
12.解:﹣2+6﹣7=﹣3,
故答案为:﹣3
13.解:∵3m=32n=2,
∴3m+2n=3m•32n=2×2=4,
故答案为:4
14.解:如图,作AH⊥BC于H.
在Rt△ACH中,∵∠AHC=90°,AC=2,COSC=,
∴=,
∴CH=,
∴AH===,
在Rt△ABH中,∵∠AHB=90°,∠B=30°,
∴AB=2AH=,
故答案为.
15.解:∵PQ⊥x轴,
∴设P(x,),则Q(x,x﹣2),
∴PQ=﹣x+2,
∴S△POQ=(﹣+2)•x=﹣(x﹣2)2+3,
∵﹣<0,
∴△POQ面积有最大值,最大值是3,
故答案为3.
16.解:∵∠B=30°,直线l⊥AB,
∴BE=2EF,
由图可得,
AB=4cos30°=4×=2,
BC=5,
AD=7﹣4=3,
当EF平移到点F与点D重合时,如右图所示,
∵∠EFB=60°,
∴∠DEC=60°,
∵DE=CE=2,
∴△DEC为等边三角形,
∴CD=2.
∴四边形ABCD的周长是:AB+BC+AD+CD=2+5+3+2=10+2,
故答案为:10+2.
三、本大题共3个小题,每小题9分,共27分.
17.解:原式=,
=2﹣1+1,
=2.
18.解:根据题意得:,
去分母,得x=2(x+1),
去括号,得x=2x+2,
解得x=﹣2
经检验,x=﹣2是原方程的解.
19.证明:在△AEB和△DEC中,
∵
∴△AEB≌△DEC,
∴∠B=∠C.
四、本大题共3个小题,每小题10分,共30分.
20.解:原式=÷,
=×,
=.
21.解:(1)∵点P(﹣1,a)在直线l2:y=2x+4上,
∴2×(﹣1)+4=a,即a=2,
则P的坐标为(﹣1,2),
设直线l1的解析式为:y=kx+b(k≠0),
那么,
解得:.
∴l1的解析式为:y=﹣x+1.
(2)∵直线l1与y轴相交于点C,
∴C的坐标为(0,1),
又∵直线l2与x轴相交于点A,
∴A点的坐标为(﹣2,0),则AB=3,
而S四边形PAOC=S△PAB﹣S△BOC,
∴S四边形PAOC=.
22.解:(1)男生:1+2+2+4+9+14+5+2+1=40(人)
女生:1+1+2+3+11++13+7+1+1=40(人)
故答案为40,40;
(2)女生成绩27的人数最多,所以众数为27,
故答案为27;
(3)(人),
七年级720名学生中成绩为优秀的学生人数大约是396人.
五、本大题共2个小题,每小题10分,共20分.
23.(1)证明:∵△=(k+4)2﹣16k=k2﹣8k+16=(k﹣4)2≥0,
∴无论k为任何实数时,此方程总有两个实数根;
(2)解:由题意得:x1+x2=k+4,x1•x2=4k,
∵,
∴,
即,
解得:k=2;
(3)解:解方程x2﹣(k+4)x+4k=0得:x1=4,x2=k,
根据题意得:42+k2=52,即k=3,
设直角三角形ABC的内切圆半径为r,如图,
由切线长定理可得:(3﹣r)+(4﹣r)=5,
∴直角三角形ABC的内切圆半径r=.
24.(1)证明:如图,连结OB,则OP=OB,
∴∠OBP=∠OPB=∠CPA,
AB=AC,
∴∠ACB=∠ABC,
而OA⊥l,即∠OAC=90°,
∴∠ACB+∠CPA=90°,
即∠ABP+∠OBP=90°,
∴∠ABO=90°,
OB⊥AB,
故AB是⊙O的切线;
(2)解:由(1)知:∠ABO=90°,
而OA=5,OB=OP=3,
由勾股定理,得:AB=4,
过O作OD⊥PB于D,则PD=DB,
∵∠OPD=∠CPA,∠ODP=∠CAP=90°,
∴△ODP∽△CAP,
∴,
又∵AC=AB=4,AP=OA﹣OP=2,
∴,
∴,
∴.
六、本大题共2个小题,第25题12分,第26题13分,共25分.
25.(1)证明:∵G是△ABC重心,
∴,
又∵EF∥BC,
∴,,
则;
(2)解:(1)中结论成立,理由如下:
如图2,过点A作AN∥BC交EF的延长线于点N,FE、CB的延长线相交于点M,
则△BME∽△ANE,△CMF∽△ANF,
,,
∴,
又∵BM+CM=BM+CD+DM,
而D是BC的中点,即BD=CD,
∴BM+CM=BM+BD+DM=DM+DM=2DM,
∴,
又∵,
∴,
故结论成立;
(3)解:(1)中结论不成立,理由如下:
当F点与C点重合时,E为AB中点,BE=AE,
点F在AC的延长线上时,BE>AE,
∴,则,
同理:当点E在AB的延长线上时,,
∴结论不成立.
26.解:
(1)根据题意得:A(﹣2,0),B(6,0),
在Rt△AOC中,∵,且OA=2,得CO=3,∴C(0,3),将C点坐标代入y=a(x+2)(x﹣6)得:,
抛物线解析式为:;
整理得:y=﹣
故抛物线解析式为:得:y=﹣;
(2)
①由(1)知,抛物线的对称轴为:x=2,顶点M(2,4),设P点坐标为(2,m)(其中0≤m≤4),
则PC2=22+(m﹣3)2,PQ2=m2+(n﹣2)2,CQ2=32+n2,∵PQ⊥PC,∴在Rt△PCQ中,由勾股定理得:PC2+PQ2=CQ2,
即22+(m﹣3)2+m2+(n﹣2)2=32+n2,整理得:=(0≤m≤4),∴当时,n取得最小值为;当m=4时,n取得最大值为4,
所以,;
②
由①知:当n取最大值4时,m=4,
∴P(2,4),Q(4,0),
则,,CQ=5,
设点P到线段CQ距离为h,
由,
得:,故点P到线段CQ距离为2;
③由②可知:当n取最大值4时,Q(4,0),∴线段CQ的解析式为:,
设线段CQ向上平移t个单位长度后的解析式为:,
当线段CQ向上平移,使点Q恰好在抛物线上时,线段CQ与抛物线有两个交点,此时对应的点Q'的纵坐标为:,
将Q'(4,3)代入得:t=3,
当线段CQ继续向上平移,线段CQ与抛物线只有一个交点时,
联解
得:,化简得:x2﹣7x+4t=0,
由△=49﹣16t=0,得,∴当线段CQ与抛物线有两个交点时,.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/6/24 9:38:55;用户:15708455779;邮箱:15708455779;学号:24405846
四川省乐山市中考数学试卷(含解析版): 这是一份四川省乐山市中考数学试卷(含解析版),共30页。试卷主要包含了选择题,填空题,每小题9分,共27分,每小题10分,共30分,每小题10分,共20分等内容,欢迎下载使用。
2023年四川省乐山市中考数学试卷(含答案解析): 这是一份2023年四川省乐山市中考数学试卷(含答案解析),共23页。试卷主要包含了 计算, 下面几何体中,是圆柱的为等内容,欢迎下载使用。
2023年四川省乐山市中考数学试卷(含答案解析): 这是一份2023年四川省乐山市中考数学试卷(含答案解析),共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












