苏科版数学九年级上册期中复习试卷05（含答案）

苏科版数学九年级上册期中复习试卷

一、选择题

1.下列方程中是关子的一元二次方程的是( ▲ )

  A.           B.     

  C.       D.

2.已知二次函数，下列说法正确的是( ▲ )

  A．开口向上，顶点坐标                B．开口向下，顶点坐标

  C．开口向上，顶点坐标             D．开口向下，顶点坐标

3.在平面直角坐标系中，将二次函数的图像向上平移2个单位，所得图像的解析式为( ▲ )

  A.          B.       

  C.         D.

4.当用配方法解一元二次方程x2－3＝4x时，下列方程变形正确的是 ( ▲ )

  A．(x—2)2＝2         B．(x一2)2＝4        C．(x－2)2＝1        D．(x－2)2＝7

5.关于的一元二次方程有两个相等的实数根，则的值为( ▲ )

A．                 B．               C．               D．

6.已知⊙O的半径为5cm，点P不在⊙O外，则线段OP的长( ▲ )

  A．小于5cm          B．不大于5cm        C．小于10cm         D．不大于10cm 

7.下列说法：①半径为3cm且经过点P的圆有无数个；②直径是圆的对称轴；③菱形的四个顶点在同一个圆上；④平分弦的直径垂直于这条弦.其中真命题有( ▲ )个.

  A.  1个              B.  2个              C.  3个              D.  4个

      （第8题图）                                （第9题图）

8.如图，AB是⊙O的直径，点C、D在⊙O上，∠BOC=112°，AD∥OC，则∠AOD=( ▲ )

  A．14°               B．24°               C．34°              D．44°

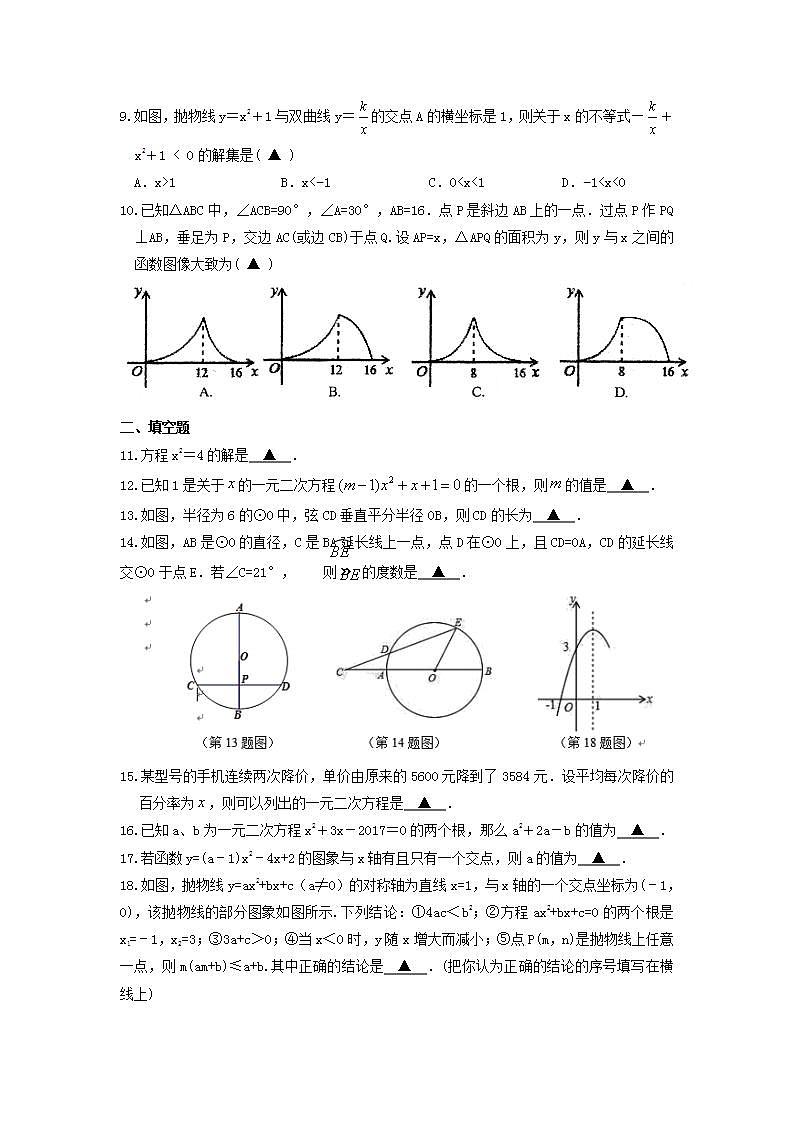
9.如图，抛物线y＝x2＋1与双曲线y＝的交点A的横坐标是1，则关于x的不等式—＋x2＋1 < 0的解集是( ▲ )

  A．x>1               B．x<−1              C．0<x<1           D．−1<x<0

10.已知△ABC中，∠ACB=90°，∠A=30°，AB=16．点P是斜边AB上的一点．过点P作PQ⊥AB，垂足为P，交边AC(或边CB)于点Q.设AP=x，△APQ的面积为y，则y与x之间的函数图像大致为( ▲ )

二、填空题

11.方程x2＝4的解是  ▲  ．

12.已知1是关于的一元二次方程的一个根，则的值是  ▲  ．

13.如图，半径为6的⊙O中，弦CD垂直平分半径OB，则CD的长为  ▲  ．

14.如图，AB是⊙O的直径，C是BA延长线上一点，点D在⊙O上，且CD=OA，CD的延长线交⊙O于点E．若∠C=21°，    则的度数是  ▲  ．

15.某型号的手机连续两次降价，单价由原来的5600元降到了3584元．设平均每次降价的百分率为，则可以列出的一元二次方程是  ▲  ．

16.已知a、b为一元二次方程x2＋3x－2017＝0的两个根，那么a2＋2a－b的值为  ▲  ．

17.若函数y=(a﹣1)x2﹣4x+2的图象与x轴有且只有一个交点，则a的值为  ▲  ．

18.如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为(﹣1，0)，该抛物线的部分图象如图所示.下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③3a+c＞0；④当x＜0时，y随x增大而减小；⑤点P(m，n)是抛物线上任意一点，则m(am+b)≤a+b.其中正确的结论是  ▲  ．(把你认为正确的结论的序号填写在横线上)

三．解答题

19.解方程：

(1) （用配方法解）   (2)     (3)   

20.已知抛物线，直线y=x. 求证：抛物线和直线总有交点.

21.已知关于x的一元二次方程有两个不相等的实数根．

 (1)求的取值范围；

 (2)等腰中，，若、的长是方程的两根，求BC的长．

22.如图，已知⊙O中，点A、B、C、D在圆上，且AB=CD，求证：AC=BD.

23.如图，已知⊙O中直径AB和弦AC交于点A，点D、E分别是半圆AB和的中点，连接DE分别交AB、AC于点F、G.

   (1)求证：AF=AG；

   (2)连接CE. 若AF=4，BF=6，∠A=30°.求弦CE的长.

24.已知关于x的一元二次方程x2－2(m－1)x＋m2＝0有两个实数根x1，x2．

   (1)求m的取值范围；

   (2)若|x1＋x2|＝x1x2－1，求m的值．

25.如图，二次函数的图象经过A、B、C三点．

  (1)观察图象，直接写出：当满足   ▲   时，抛物线在直线AC的上方.

   (2)求抛物线的解析式；

   (3)观察图象，直接写出：当满足   ▲   时，y<0；

(4)若抛物线上有两个动点，请比较和的大小.

26.如图，某农场老板准备建造一个矩形养兔场ABCD，他打算让矩形养兔场的一边完全靠着墙   MN，墙MN可利用的长度为24米，另外三边用长度为50米的篱笆围成（篱笆正好要全部用完，且不考虑接头的部分）.

   (1)若要使矩形养兔场的面积为300平方米，则垂直于墙的一边长AB为多少米？

(2)该矩形养兔场ABCD的面积有最大值吗？若有最大值，请求出面积最大时AB的长度；若没有最大值，请说明理由.

27.如图①，抛物线（a≠0）与x轴交于点A和点B，与y轴交于点C，且OC=OB．

   (1)直接写出点B的坐标是(  ▲  ，  ▲  )，并求抛物线的解析式；

   (2)设点D是抛物线的顶点，抛物线的对称轴是直线l，如图②.连接BD，线段OC上的点E关于直线l的对称点E'恰好在线段BD上，求点E的坐标；

   (3)若点F为抛物线第二象限图象上的一个动点，如图③.连接BF、CF.当△BCF的面积是△ABC面积的一半时，求此时点F的坐标．

             图①                           图②                         图③

28.如图①，二次函数的图象与x轴交于A(3，0)、B(﹣1，0)两点，与y轴交于点C．在x轴上有一个动点D(m，0)，其中0<m<3．

   (1)求抛物线的解析式；

   (2)过点D作x轴的垂线交直线AC于点E，交抛物线于点F，过点F作FG⊥AC于点G．设△ADE的周长为C1，△EFG的周长为C2，若，求m的值；

   (3)如图②，动点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB、AC边运动，其中一点到达端点时，另一点也随之停止运动.当P、Q运动到t秒时，△APQ沿PQ所在的直线翻折，点A恰好落在抛物线上H点处，请直接判定此时四边形APHQ的形状，并求出点H坐标．

                           图①                        图②

数学答案

1-10  CABDC  BADCB

11、                        12、              13、                  14、63°

15、                           16、               17、                 18、①②⑤

三、解答题

19、（1）                              （2）                      

                             1'                                  

（3）

20、将直线、抛物线解析式联立，得                                        

所以抛物线和直线总有交点.

21、（1）             

（2）将x=2代入方程，得k=   ，  所以方程为                ，解得             

所以       

22、证明：∵AB=CD  ∴弧AB=弧CD  

         ∵弧BC=弧BC  ∴弧BC+弧AB=弧BC+弧CD   即：弧AC=弧BD 5' ∴AC=BD.

23、（1）连接OD、OE，交AC于点H；证明⊿DFO～⊿EGH；得∠DFO=∠EGH  1'(用三角形内角和得出也可以)

         从而得∠AFG=∠AGF，所以 AF=AG.   

    （2）半径5        EH=2.5     从而能求出CE=5   

24、（1）           （列出⊿的式子可得1分）

     （2）由      得m-1<0         x1＋x2=2（m-1）, x1x2=

          |x1＋x2|＝x1x2－1可得2（1-m）=-1        m=—3 

25、（1）x>4或x<—1                                

    （2）                          

    （3）                                     

    （4）

26、（1）设AB=x,根据题意得：x(50-2x)=300,  x1=15,x2=10(舍去)   所以：AB=15 

     （2）因为50-2x≤24  所以x≥13.   

          假设矩形场地面积为y=x(50-2x) =   所以AB=13.  

27、（1）             1             

    （2）               

    （3）求出三角形ABC面积                         

28、（1）

    （2）          

    （3）菱形                    H的横坐标求出可得1分