

专题13双曲线 题型归纳讲义-2022届高三数学一轮复习(解析版)学案
展开专题十三《解析几何》讲义
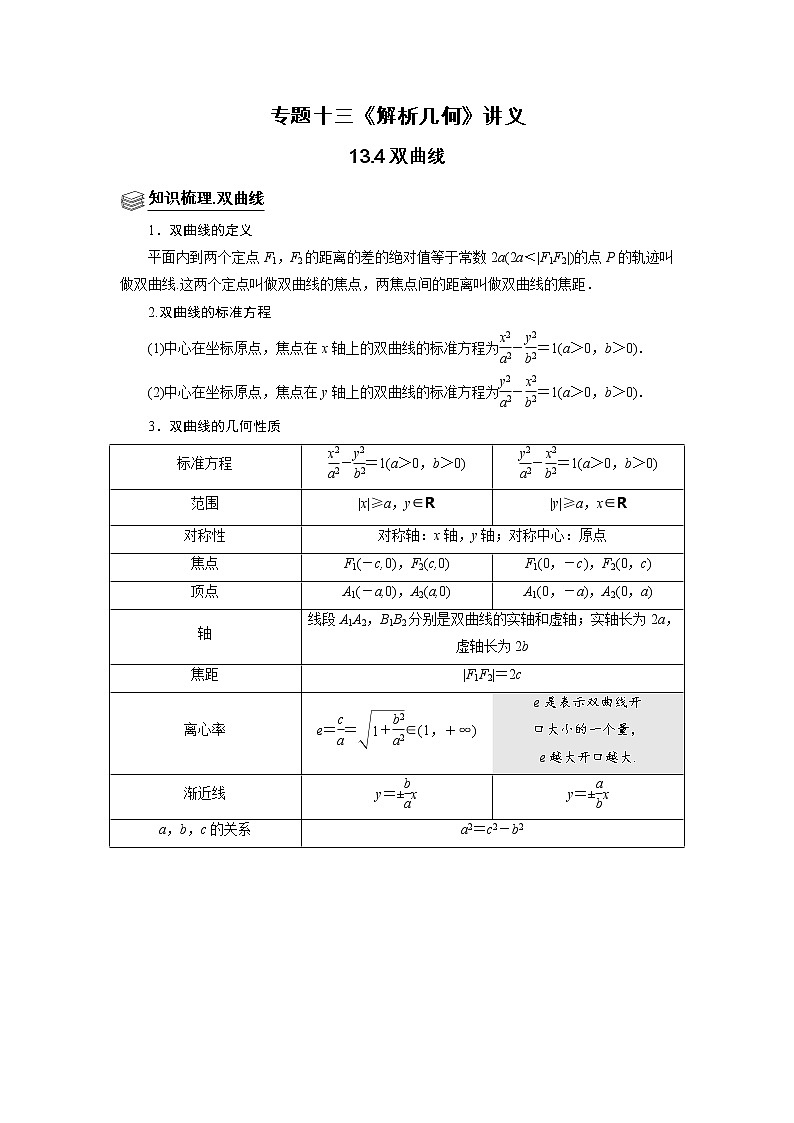
13.4双曲线
知识梳理.双曲线
1.双曲线的定义
平面内到两个定点F1,F2的距离的差的绝对值等于常数2a(2a<|F1F2|)的点P的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
2.双曲线的标准方程
(1)中心在坐标原点,焦点在x轴上的双曲线的标准方程为-=1(a>0,b>0).
(2)中心在坐标原点,焦点在y轴上的双曲线的标准方程为-=1(a>0,b>0).
3.双曲线的几何性质
标准方程
-=1(a>0,b>0)
-=1(a>0,b>0)
范围
|x|≥a,y∈R
|y|≥a,x∈R
对称性
对称轴:x轴,y轴;对称中心:原点
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
轴
线段A1A2,B1B2分别是双曲线的实轴和虚轴;实轴长为2a,虚轴长为2b
焦距
|F1F2|=2c
离心率
e==∈(1,+∞)
e是表示双曲线开
口大小的一个量,
e越大开口越大.
渐近线
y=±x
y=±x
a,b,c的关系
a2=c2-b2
题型一.双曲线及其性质
1.过双曲线x24-y23=1左焦点F的直线交双曲线的左支于M、N两点,F2为其右焦点,则|MF2|+|NF2|﹣|MN|的值为 8 .
【解答】解:根据双曲线定义有|MF2|﹣|MF|=2a,|NF2|﹣|NF|=2a,
两式相加得|MF2|+|NF2|﹣|MN|=4a=8.
答案:8.
2.设双曲线C:x28-y2b2=1的左、右焦点分别为F1,F2,过F1的直线与双曲线C交于M,N两点,其中M在左支上,N在右支上,若点F2在线段MN的中垂线上,则MN=( )
A.82 B.8 C.42 D.4
【解答】解:如图,由双曲线方程可得a=22.
由双曲线的定义可知:|F2M|﹣|F1M|=2a=42,
|F1N|﹣|F2N|=2a=42,
∴|F2M|=|F1M|+42,|F1N|=|F2N|+42,
∵点F2在线段MN的中垂线上,∴|F2M|=|F2N|,
∴|F1N|=|F1M|+82,
∴|MN|=|F1N|﹣|F1M|=82.
故选:A.
3.过双曲线C:x2a2-y2b2=1的右顶点作x轴的垂线与C的一条渐近线相交于A,若以C的右焦点为圆心、半径为2的圆经过A、O两点(O为坐标原点),则双曲线C的标准方程是 x2-y23=1 .
【解答】解:双曲线的右顶点为(a,0),右焦点F为(c,0),
由x=a和一条渐近线y=bax,可得A(a,b),
以C的右焦点为圆心、半径为2的圆经过A、O两点(O为坐标原点),
则|AF|=|OF|=c=2,
即有(a-c)2+b2=2,
c2=a2+b2=4,
解得a=1,b=3,
即有双曲线的方程为x2-y23=1,
故答案为:x2-y23=1.
4.P是双曲线x29-y216=1的右支上一点,M、N分别是圆(x+5)2+y2=4和(x﹣5)2+y2=1上的点,则|PM|﹣|PN|的最大值为 9 .
【解答】解:双曲线x29-y216=1中,
∵a=3,b=4,c=5,
∴F1(﹣5,0),F2(5,0),
∵|PF1|﹣|PF2|=2a=6,
∴|MP|≤|PF1|+|MF1|,|PN|≥|PF2|﹣|NF2|,
∴﹣|PN|≤﹣|PF2|+|NF2|,
所以,|PM|﹣|PN|≤|PF1|+|MF1|﹣|PF2|﹣|NF2|
=6+1+2
=9.
故答案为:9.
5.已知F是双曲线C:x2-y28=1的右焦点,P是C的左支上一点,A(0,66).当△APF周长最小时,该三角形的面积为 126 .
【解答】解:由题意,设F′是左焦点,则△APF周长=|AF|+|AP|+|PF|=|AF|+|AP|+|PF′|+2
≥|AF|+|AF′|+2(A,P,F′三点共线时,取等号),
直线AF′的方程为x-3+y66=1与x2-y28=1联立可得y2+66y﹣96=0,
∴P的纵坐标为26,
∴△APF周长最小时,该三角形的面积为12×6×66-12×6×26=126.
故答案为:126.
题型二.焦点三角形
1.已知点F1,F2分别为双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点,过F1的直线交双曲线C的左支于A,B两点,且|AF2|=3,|BF2|=5,|AB|=4,则△BF1F2的面积为 92 .
【解答】解:|AF2|=3,|BF2|=5,|AB|=4,
可得三角形ABF2为直角三角形,∠BAF2=90°,
设|AF1|=m,|BF1|=n,可得m+n=4,
3﹣m=5﹣n=2a,解得m=1,n=3,
则△BF1F2的面积为S△ABF2-S△AF1F2=12×3×4-12×1×3=92.
故答案为:92.
2.已知F1,F2是双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点,P是双曲线右支上任意一点,M是线段PF1的中点,则以PF1为直径的圆与圆x2+y2=a2的位置关系是( )
A.相离 B.相切
C.相交 D.以上都有可能
【解答】解:∵P在双曲线右支上,∴|PF1|﹣|PF2|=2a,
∵M是线段PF1的中点,∴|MF1|=|PM|=12|PF1|,
∵O是线段F1F2的中点,∴|MO|=12|PF2|,
∴12|PF1|-12|PF2|=a⇒|MF1|-|OM|=a⇒|OM|=|MF1|-a,
即圆心距等于两圆的半径之差,
∴以线段PF1为直径的圆与圆x2+y2=a2的位置关系是相内切.
故选:B.
3.已知双曲线C:x22-y2=1的左右焦点为F1、F2,点M为双曲线C上任一点,则|MF1|•|MF2|的最小值为( )
A.1 B.2 C.2 D.3
【解答】解:根据题意可得F1(-3,0),F2(3,0),设M(x,y),其中x(﹣∞,-2]∪[2,+∞),则y2=x22-1,
则|MF1|•|MF2|=(x+3)2+y2•(x-3)2+y2=(x+3)2+x22-1•(x-3)2+x22-1=(32x2-2)2,
因为x∈(﹣∞,-2]∪[2,+∞),所以32x2≥3,
则当x=±2时,|MF1|•|MF2|取最小值,最小值=(3-2)2=1,
故选:A.
4.从双曲线x2a2-y2b2=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|﹣|MT|等于( )
A.c﹣a B.b﹣a C.a﹣b D.c﹣b
【解答】解:如图所示,设F′是双曲线的右焦点,连接PF′.
∵点M,O分别为线段PF,FF′的中点,
由三角形中位线定理得到:|OM|=12|PF′|=12(|PF|﹣2a)=12|PF|﹣a
=|MF|﹣a,
∴|OM|﹣|MT|=|MF|﹣|MT|﹣a=|FT|﹣a,连接OT,因为PT是圆的切线,
则OT⊥FT,
在Rt△FOT中,|OF|=c,|OT|=a,
∴|FT|=丨OF丨2-丨OT丨2=b.
∴|OM|﹣|MT|=b﹣a.
故选:B.
题型三.渐近线性质
1.过双曲线C:x2a2-y2b2=1的右顶点作x轴的垂线,与C的一条渐近线相交于点A.若以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )
A.x212-y24=1 B.x27-y29=1
C.x28-y28=1 D.x24-y212=1
【解答】解:∵以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),
∴半径R=c=4,则圆的标准方程为(x﹣4)2+y2=16,
设B(a,0),y=ba⋅a=b,即A(a,b),
则(a﹣4)2+b2=16,
即a2﹣8a+16+b2=16,
即c2﹣8a=0,即8a=16,
则a=2,b2=16﹣4=12,
则双曲线C的方程为x24-y212=1,
故选:D.
2.设F1,F2是双曲线C:x2a2-y2b2=1(a>0,b>0)的左,右焦点,O是坐标原点.过F2作C的一条渐近线的垂线,垂足为P,若|PF1|=6|OP|,则C的离心率为 3 .
【解答】解:双曲线C:x2a2-y2b2=1(a>0.b>0)的一条渐近线方程为y=bax,
∴点F2到渐近线的距离d=bca2+b2=b,即|PF2|=b,
∴|OP|=|OF2|2-|PF2|2=c2-b2=a,cos∠PF2O=bc,
∵|PF1|=6|OP|,
∴|PF1|=6a,
在三角形F1PF2中,由余弦定理可得|PF1|2=|PF2|2+|F1F2|2﹣2|PF2|•|F1F2|COS∠PF2O,
∴6a2=b2+4c2﹣2×b×2c×bc=4c2﹣3b2=4c2﹣3(c2﹣a2),
即3a2=c2,得e=3,
故答案为:3.
3.已知斜率为1的直线l与双曲线x2a2-y2b2=1(a>0,b>0)相交于A,B两点,且AB的中点为M(1,3),则双曲线的渐近线方程为( )
A.y=±3x B.y=±3x C.y=±13x D.y=±33x
【解答】解:设A(x1,y1),B(x2,y2),则x12a2-y12b2=1,x22a2-y22b2=1
两式相减可得:(x1+x2)(x1-x2)a2-(y1+y2)(y1-y2)b2=0,
∵斜率为1的直线l与双曲线x2a2-y2b2=1(a>0,b>0)相交于A,B两点,A、B的中点为M(1,3),
∴k•kOM=b2a2=3,
∴y=±bax=±3x.
故选:B.
4.已知双曲线x2a2-y2b2=1(a>0,b>0)的右焦点为F,若过F且倾斜角为60°的直线分别与双曲线的左右两支相交,则此双曲线离心率的取值范围是 (2,+∞) .
【解答】解:依题意,斜率为3的直线l过双曲线x2a2-y2b2=1(a>0,b>0)
的右焦点为F且与双曲线的左右两支分别相交,
结合图形分析可知,
双曲线的一条渐近线的斜率ba必大于3,
即ba>3,
因此该双曲线的离心率e=ca=1+(ba)2>1+3=2.
故答案为:(2,+∞).
题型四.构建等量关系求离心率
1.设双曲线x2a2-y2b2=1(a>0,b>0)的右焦点是F,左、右顶点分别是A1,A2,过F做x轴的垂线交双曲线于B,C两点,若A1B⊥A2C,则双曲线的离心率为 2 .
【解答】解:由题意可知:左、右顶点分别是A1(﹣a,0),A2(a,0),
当x=c时,代入双曲线方程,解得:y=±b2a,
设B(c,b2a),C(c,-b2a),
则直线A1B的斜率k1=b2a-0c-(-a)=b2a(c+a),
直线A2C的斜率k2=-b2a-0c-a=-b2a(c-a),
由A1B⊥A2C,则k1×k2=﹣1,即b2a(c+a)×b2a(c-a)=1,
则b2a2=1,
双曲线的离心率e=ca=1+b2a2=2,
故答案为:2.
2.过双曲线M:x2-y2b2=1的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是( )
A.10 B.5 C.103 D.52
【解答】解:过双曲线M:x2-y2b2=1的左顶点A(﹣1,0)作斜率为1的直线l:y=x+1,
若l与双曲线M的两条渐近线x2-y2b2=0分别相交于点B(x1,y1),C(x2,y2),
联立方程组x2-y2b2=0y=x+1
代入消元得(b2﹣1)x2﹣2x﹣1=0,
∴x1+x2=2b2-1x1x2=11-b2,
∴x1+x2=﹣2x1x2,
又|AB|=|BC|,则B为AC中点,2x1=﹣1+x2,
代入解得x1=-14x2=12,
∴b2=9,双曲线M的离心率e=ca=10,
故选:A.
3.已知F1、F2是双曲线x2a2-y2b2=1(a>0,b>0)的两个焦点,以线段F1F2为边作正△MF1F2,若边MF1的中点在双曲线时,双曲线的离心率e= 3+1 .
【解答】解:以线段F1F2为边作正△MF1F2,则M在y轴上,
可设|F1F2|=2c,则M(0,3c),
又F1(﹣c,0),则边MF1的中点为(-c2,32c),
代入双曲线方程,可得,
c24a2-3c24b2=1,由于b2=c2﹣a2,e=ca,
则有e2-3e2e2-1=4,即有e4﹣8e2+4=0,
解得,e2=4±23,由于e>1,即有e=1+3.
故答案为:1+3.
4.(2019·全国卷Ⅰ)已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A、B两点.若F1A→=AB→,F1B→⋅F2B→=0,则双曲线C的离心率为( )
A.233 B.2 C.2 D.3
【解答】解:∵F1A→=AB→,OF1=OF2,∠BF1F2=∠BF1F2,
∴△AF1O∽△BF1F2,
又∵F1B→⋅F2B→=0,
∴OA⊥F1B,
∴kF1B⋅(-ba)=-1,即kF1B=ab,
∴直线F1B的方程为y=ab(x+c),
联立直线F1B与渐近线y=bax,即y=ab(x+c)y=bax,解得B(a2cb2-a2,abcb2-a2),
∵OB=12F1F2=c,
∴a4c2(b2-a2)2+a2b2c2(b2-a2)2=c2,化简可得b2=3a2,
由双曲线的性质,可得c2﹣a2=b2=3a2,即c2=4a2,
∴c=2a,
∴e=ca=2.
故选:C.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
题型五.离心率的取值范围
1.设点P在双曲线x2a2-y2b2=1(a>0,b>0)的右支上,双曲线的左、右焦点分别为F1,F2,若|PF1|=4|PF2|,则双曲线离心率的取值范围是( )
A.(1,53] B.(1,2] C.[53,+∞) D.[2,+∞)
【解答】解:∵|PF1|=4|PF2|,
∴由双曲线的定义可得|PF1|﹣|PF2|=3|PF2|=2a,
∴|PF2|=23a,
∵点P在双曲线的右支上,
∴|PF2|≥c﹣a,
∴23a≥c﹣a,即53a≥c,
∴e=ca≤53,
∵e>1,
∴1<e≤53,
∴双曲线的离心率e的取值范围为(1,53].
故选:A.
2.已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左右焦点分别为F1,F2,O为坐标原点,点M为双曲线右支上一点,若|F1F2|=2|OM|,tan∠MF2F1≥2,则双曲线C的离心率的取值范围为 (1,5] .
【解答】解:法一:∵|F1F2|=2|OM|,∴∠F1MF2=π2,
∴4c2=|MF1|2+|MF2|2,tan∠MF2F1=|MF1||MF2|,
∵|MF1|﹣|MF2|=2a,
∴e2=4c24a2=|MF1|2+|MF2|2(|MF1|-|MF2|)2=|MF1|2+|MF2|2|MF2|2|MF1|2-2|MF1||MF2|+|MF2|2|MF2|2,
设|MF1||MF2|=t≥2,则e2=t2+1t2-2t+1=1+2t+1t-2,
∴t+1t≥2+12=52,∴1<e2≤5,∴1<e≤5.
法二:∵|F1F2|=2|OM|,∴∠F1MF2=π2,令|MF1|=r1,|MF2|=r2,
∠MF2F1=θ,tanθ≥2,r1=2csinθ,r2=2ccosθ,
∴2a=r1﹣r2=2c(sinθ﹣cosθ),∴e=1sinθ-cosθ,∴e2=1(sinθ-cosθ)2=11-sin2θ=11-2tanθ1+tan2θ≤5,
∴1<e≤5.
故答案为:(1,5].
3.F1,F2是双曲线x2a2-y2b2=1(a>0,b>0)的左右焦点,若双曲线上存在点P满足PF1→⋅PF2→=-a2,则双曲线离心率的取值范围为( )
A.[3,+∞) B.[2,+∞) C.(1,3] D.(1,2]
【解答】解:设PF1=r1,PF2=r2,则PF1→⋅PF2→=-a2⇔r1r2cos∠F1PF2=﹣a2,
再根据余弦定理得r1r2•r12+r22-4c22r1r2=-a2,即r12+r22=4c2﹣2a2,①,
又由双曲线的定义可得:|r1﹣r2|=2a,即r12+r22﹣2r1r2=4a2,②
又r1+r2≥2c,即r12+r22+2r1r2≥4c2,③
②+③得2(r12+r22)≥4a2+4c2,将①代入得:2(4c2﹣2a2)≥4a2+4c2,
化简得:c2≥2a2,∴e2≥2,∴e≥2.
故选:B.
课后作业.双曲线
1.已知F1,F2是双曲线E:x2a2-y2b2=1(a>0,b>0)的左右焦点,F2与抛物线C:y2=43x的焦点重合,点M在E上,MF2与x轴垂直,|MF2|=2,则E的离心率为( )
A.2 B.32 C.3 D.2
【解答】解:F2与抛物线C:y2=43x的焦点重合,
则F2(3,0),
即c=3,
∴|F1F2|=2c=23,
∵MF2与x轴垂直,|MF2|=2,
∴|MF1|=2a+2,
∴(2a+2)2=22+(23)2,
解得a=1,
∴e=ca=3,
故选:C.
2.已知M(x0,y0)是双曲线C:x22-y2=1上的一点,F1、F2是C上的两个焦点,若∠F1MF2为钝角,则y0的取值范围是 (-33,0)∪(0,33) .
【解答】解:由题意,∵∠F1MF2为钝角,
∴MF1→•MF2→=(-3-x0,﹣y0)•(3-x0,﹣y0)=x02﹣3+y02=3y02﹣1<0,且3y02﹣1≠﹣1
∴-33<y0<33且y0≠﹣1.
∴y0的取值范围是(-33,0)∪(0,33).
故答案为:(-33,0)∪(0,33).
3.设F1、F2分别为双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点,过F1的直线l与圆O:x2+y2=a2相切,l与C的渐近线在第一象限内的交点是P,若PF2⊥x轴,则双曲线的离心率等于( )
A.3 B.2 C.22 D.4
【解答】解:依题意双曲线的渐近线方程:ax﹣by=0,因为PF2⊥x轴,可得
P(c,bca),直线PF1:的斜率为:k=bcac+c=b2a,直线方程为:y=b2a(x+c),直线与圆x2+y2=a2相切,
所以bc2a1+(b2a)2=a,
整理得:
(bc)2=a2(4a2+b2),则c4﹣2a2c2﹣3a4=0,即e4﹣2e2﹣3=0,
e>1,
解得e=3,
故选:A.
4.已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左右焦点分别为F1,F2,点O为坐标原点,点P在双曲线的右支上,且满足|F1F2|=2|OP|.若直线PF2与双曲线C只有一个交点,则双曲线C的离心率为( )
A.2 B.3 C.5 D.6
【解答】解:双曲线C:x2a2-y2b2=1(a>0,b>0)的左右焦点分别为F1,F2,点O为坐标原点,点P在双曲线的右支上,
且满足|F1F2|=2|OP|.可得PF1⊥PF2,直线PF2与双曲线C只有一个交点,
可得PF2的斜率:-ba,设PF1=m,PF2=n,可得mn=ba,m﹣n=2a,m2+n2=4c2,
消去m,n,可得:a2(b-a)2=1,解得b=2a,即c2﹣a2=4a2,
所以双曲线的离心率为:e=ca=5.
故选:C.
5.已知双曲线C:x2a2-y2b2=1(a>0,b>0)的一个焦点为F,点A,B是C的一条渐近线上关于原点对称的两点,以AB为直径的圆过F且交C的左支于M,N两点,若|MN|=2,△ABF的面积为8,则C的渐近线方程为( )
A.y=±3x B.y=±33x C.y=±2x D.y=±12x
【解答】解:设双曲线的另一个焦点为F',由双曲线的对称性,可得四边形AFBF'是矩形,
∴S△ABF=S△ABF',
即bc=8,
由x2+y2=c2x2a2-y2b2=1,可得y=±b2c,
则|MN|=2b2c=2,即b2=c,
∴b=2,c=4,
∴a=c2-b2=23,
∴C的渐近线方程为y=±33x,
故选:B.
6.过双曲线x2a2-y2b2=1(a>0,b<0)的右焦点且垂直于x轴的直线与双曲线交于A,B两点,与双曲线的渐近线交于C,D两点,若|AB|≥513|CD|,则双曲线离心率的取值范围为 [1312,+∞) .
【解答】解:易知|AB|=2b2a,因为渐近线y=±bcx,所以|CD|=2bca,
由2b2a≥513⋅2bca化简得b≥513c,即b2≥25169c2,
所以c2-a2≥25169c2,从而(ca)2≥169144,
解得ca≥1312.
故答案为:[1312,+∞).
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/8/20 22:31:13;用户:15942715433;邮箱:15942715433;学号:32355067
专题13直线方程 题型归纳讲义-2022届高三数学一轮复习(解析版)学案: 这是一份专题13直线方程 题型归纳讲义-2022届高三数学一轮复习(解析版)学案,共13页。
专题13椭圆 题型归纳讲义-2022届高三数学一轮复习(解析版)学案: 这是一份专题13椭圆 题型归纳讲义-2022届高三数学一轮复习(解析版)学案,共21页。
专题13抛物线 题型归纳讲义-2022届高三数学一轮复习(解析版)学案: 这是一份专题13抛物线 题型归纳讲义-2022届高三数学一轮复习(解析版)学案,共21页。












