2022届高三统考数学（文科）人教版一轮复习学案：2.1 函数及其表示

这是一份2022届高三统考数学（文科）人教版一轮复习学案：2.1 函数及其表示，共8页。学案主要包含了知识重温，小题热身等内容，欢迎下载使用。


【知识重温】
一、必记3个知识点
1．函数与映射的概念
2.函数的有关概念
(1)函数的定义域、值域
在函数y＝f(x)，x∈A中，x叫做自变量，x的取值范围A叫做函数的⑥________；与x的值相对应的y值叫做函数值，函数值的集合{f(x)|x∈A}叫做函数的⑦________.显然，值域是集合B的子集．
(2)函数的三要素
⑧________、⑨________和⑩________.
(3)相等函数
如果两个函数的⑪________和⑫________完全一致，那么这两个函数相等，这是判断两个函数相等的依据．
(4)函数的表示法
表示函数的常用方法有：⑬____________、⑭__________、⑮____________.
3．分段函数
(1)若函数在其定义域的不同子集上，因⑯____________不同而分别用几个不同的式子来表示，这种函数称为分段函数．
(2)分段函数的定义域等于各段函数的定义域的⑰________，其值域等于各段函数的值域的⑱________，分段函数虽由几个部分组成，但它表示的是一个函数．
二、必明3个易误点
1．解决函数的一些问题时，易忽视“定义域优先”的原则．
2．易混“函数”与“映射”的概念：函数是特殊的映射，映射不一定是函数，从A到B的一个映射，A，B若不是数集，则这个映射便不是函数．
3．易误把分段函数理解为几种函数组成．
【小题热身】
一、判断正误
1．判断下列说法是否正确(请在括号中打“√”或“×”)．
(1)f(x)＝eq \f(1,\r(x－4))＋eq \r(3－x)是一个函数．( )
(2)A＝R，B＝R，f：x→y＝eq \f(1,x－1)，表示从集合A到集合B的映射(也是函数)．( )
(3)函数f(x)的图象与直线x＝1的交点最多有2个．( )
(4)y＝2x(x∈{1,2})的值域是2,4.( )
(5)y＝ln x2与y＝2ln x表示同一函数．( )
(6)f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2＋1，－1≤x≤1，,x＋3，x>1或x<－1，))则f(－x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2＋1， －1≤x≤1，,－x＋3， x>1或x<－1.))( )
二、教材改编
2．下列函数f(x)与g(x)是同一个函数的是( )
A．f(x)＝x－1，g(x)＝eq \f(x2,x)－1 B．f(x)＝x2，g(x)＝(eq \r(x))4
C．f(x)＝x2，g(x)＝eq \r(3,x6) D．f(x)＝x，g(x)＝eq \r(x2)
3．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋12，x≤－1，,x＋1，－10，))则f(f(－2))＝________.
三、易错易混
4．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(2x，x>0，,x＋1，x≤0.))若f(a)＋f(1)＝0，则实数a的值等于( )
A．－3 B．－1
C．－1或－3 D．3
5．函数y＝x＋eq \r(2x＋1)的值域为________．
四、走进高考
6．[2019·江苏卷]函数y＝eq \r(7＋6x－x2)的定义域是________．
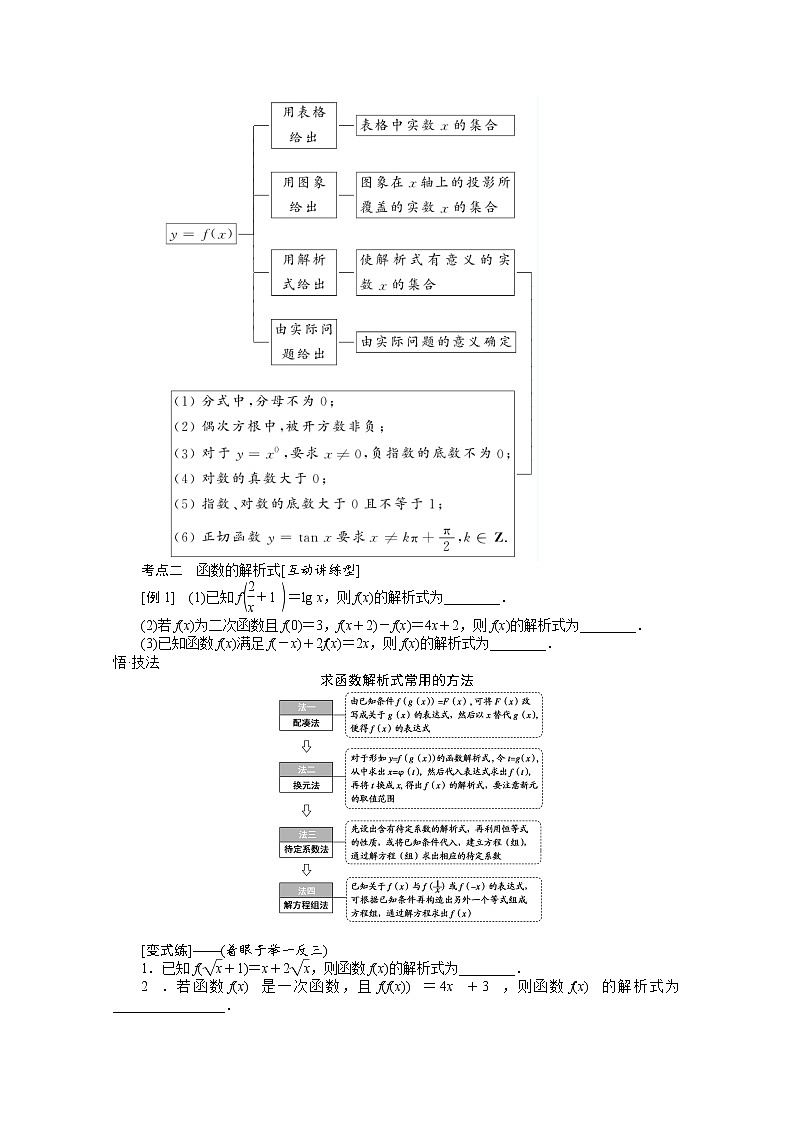
eq \x(考点一) 函数的定义域[自主练透型]
1．[2020·北京卷]函数f(x)＝eq \f(1,x＋1)＋ln x的定义域是________．
2．函数y＝eq \f(lg2－x,\r(12＋x－x2))＋(x－1)0的定义域是( )
A．{x|－3C．{x|03．[2021·抚州模拟]若函数f(x)的定义域为[0,6]，则函数eq \f(f2x,x－3)的定义域为( )
A．(0,3) B．[1,3)∪(3,8]
C．[1,3) D．[0,3)
悟·技法
考点二 函数的解析式[互动讲练型]
[例1] (1)已知feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,x)＋1))＝lg x，则f(x)的解析式为________．
(2)若f(x)为二次函数且f(0)＝3，f(x＋2)－f(x)＝4x＋2，则f(x)的解析式为________．
(3)已知函数f(x)满足f(－x)＋2f(x)＝2x，则f(x)的解析式为________．
悟·技法
求函数解析式常用的方法
[变式练]——(着眼于举一反三)
1．已知f(eq \r(x)＋1)＝x＋2eq \r(x)，则函数f(x)的解析式为________．
2．若函数f(x)是一次函数，且f(f(x))＝4x＋3，则函数f(x)的解析式为________________．
3．已知f(x)满足2f(x)＋feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)))＝3x，则f(x)＝________.
考点三 分段函数[分层深化型]
考向一：求分段函数的函数值
[例2] (1)[2021·合肥一检]已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋\f(1,x－2)，x>2，,x2＋2，x≤2，))则f(f(1))＝( )
A．－eq \f(1,2) B．2 C．4 D．11
(2)[2021·山西太原三中模拟]设函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2－1x≥2，,lg2x0考向二：分段函数与方程、不等式的综合问题
[例3] (1)设函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(4x＋a，x<1，,2x，x≥1，))若feq \b\lc\[\rc\](\a\vs4\al\c1(f\b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)))))＝4，则实数a＝( )
A．－eq \f(2,3) B．－eq \f(4,3)
C．－eq \f(4,3)或－eq \f(2,3) D．－2或－eq \f(2,3)
(2)[2018·全国卷Ⅰ]设函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(2－x，x≤0，,1，x＞0，))则满足f(x＋1)A．(－∞，－1] B．(0，＋∞)
C．(－1,0) D．(－∞，0)
悟·技法
1.求分段函数的函数值
(1)基本步骤
①确定要求值的自变量属于哪一区间．
②代入该区间对应的解析式求值．
(2)两种特殊情况
①当出现f(f(a))的形式时，应从内到外依次求值．
②当自变量的值所在区间不确定时，要分类讨论，分类标准应参照分段函数不同段的端点．
2．解分段函数与方程或不等式的综合问题的策略
求解与分段函数有关的方程或不等式问题，主要表现为解方程或不等式．应根据每一段的解析式分别求解．若自变量取值不确定，则要分类讨论求解；若自变量取值确定，则只需依据自变量的情况直接代入相应的解析式求解．解得值(范围)后一定要检验是否符合相应段的自变量的取值范围.
[同类练]——(着眼于触类旁通)
4．[2021·福州市高三质量检测]函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x，x<0,ex－1，x≥0))，则f(2)＋f(－1)＝________.
5．[2021·江西省名校高三教学质量检测]已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(2x＋12x≤0,x2－3x－3x>0))，则f(f(1))＝( )
A．－5 B．0 C．1 D．2
[变式练]——(着眼于举一反三)
6．[2021·惠州市高三第二次调研考试试题]设函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2＋x－2x≤1,1－lg xx>1))，则f(f(－4))＝________.
7．设f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(\r(x)，0A．2 B．4 C．6 D．8
[拓展练]——(着眼于迁移应用)
8．[2021·广东金山中学检测]已知f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(x,2)x≥0，,x2x<0，))则f(f(x))≥1的解集是( )
A．(－∞，－eq \r(2)] B．[4eq \r(2)，＋∞)
C．(－∞，－1]∪[4eq \r(2)，＋∞) D．(－∞，－eq \r(2)]∪[4，＋∞)
第一节 函数及其表示
【知识重温】
①非空集合 ②任意 ③唯一确定 ④任意 ⑤唯一确定 ⑥定义域 ⑦值域 ⑧定义域 ⑨值域 ⑩对应关系 ⑪定义域 ⑫对应关系 ⑬解析法 ⑭列表法 ⑮图象法 ⑯对应关系 ⑰并集 ⑱并集
【小题热身】
1．答案：(1)× (2)× (3)× (4)×
(5)× (6)√
2．解析：A中，f(x)定义域为R，g(x)的定义域为{x|x≠0}，定义域不同，∴f(x)与g(x)不是同一函数．
B中，f(x)定义域为R，g(x)定义域为{x|x≥0}，定义域不同，∴f(x)与g(x)不是同一函数．
C中，f(x)与g(x)定义域与对应关系都相同，∴f(x)与g(x)是同一函数．
D中，f(x)与g(x)定义域都是R，但对应关系不同，∴f(x)与g(x)不是同一函数．故选C.
答案：C
3．解析：∵f(－2)＝(－2＋1)2＝1，
∴f(f(－2))＝f(1)＝(1＋1)2＝4.
答案：4
4．解析：∵f(a)＋f(1)＝0，∴f(a)＝－f(1)＝－2，
当a>0时，2a＝－2，∴a＝－1(舍去)，
当a≤0时，a＋1＝－2，∴a＝－3.故选A.
答案：A
5．解析：令t＝eq \r(2x＋1)，则t≥0，且x＝eq \f(t2－1,2).
故y＝eq \f(t2－1,2)＋t＝eq \f(1,2)(t＋1)2－1，t∈[0，＋∞)．
∴y≥－eq \f(1,2).
∴函数y＝x＋eq \r(2x＋1)的值域为[－eq \f(1,2)，＋∞)．
答案：eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(1,2)，＋∞))
6．解析：由题意知7＋6x－x2≥0.
即x2－6x－7≤0.解得－1≤x≤7，
故函数的定义域为[－1,7]．
答案：[－1,7]
课堂考点突破
考点一
1．解析：函数f(x)＝eq \f(1,x＋1)＋ln x的自变量满足eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋1≠0，,x>0，))∴x>0，即定义域为(0，＋∞)．
答案：(0，＋∞)
2．解析：要使函数解析式有意义，须有eq \b\lc\{\rc\ (\a\vs4\al\c1(2－x>0，,12＋x－x2>0，,x－1≠0，))
解得eq \b\lc\{\rc\ (\a\vs4\al\c1(x<2，,－3答案：B
3．解析：因为函数f(x)的定义域为[0,6]，所以0≤2x≤6，解得0≤x≤3.又因为x－3≠0，所以函数eq \f(f2x,x－3)的定义域为[0,3)．
答案：D
考点二
例1 解析：(1)(换元法)令eq \f(2,x)＋1＝t，
得x＝eq \f(2,t－1)，因为x>0，所以t>1，
所以f(t)＝lgeq \f(2,t－1).
即f(x)的解析式是f(x)＝lgeq \f(2,x－1)(x>1)．
(2)(待定系数法)设f(x)＝ax2＋bx＋c(a≠0)，
又f(0)＝c＝3.
所以f(x)＝ax2＋bx＋3，
所以f(x＋2)－f(x)＝a(x＋2)2＋b(x＋2)＋3－(ax2＋bx＋3)＝4ax＋4a＋2b＝4x＋2.
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(4a＝4，,4a＋2b＝2，))
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝1，,b＝－1.))
所以所求函数的解析式为f(x)＝x2－x＋3.
(3)(解方程组法)因为2f(x)＋f(－x)＝2x，①
将x换成－x得2f(－x)＋f(x)＝－2x，②
由①②消去f(－x)，得3f(x)＝6x，
所以f(x)＝2x.
答案：(1)f(x)＝lgeq \f(2,x－1)(x>1)
(2)f(x)＝x2－x＋3 (3)f(x)＝2x
变式练
1．解析：解法一(配凑法) ∵f(eq \r(x)＋1)＝x＋2eq \r(x)＝(eq \r(x))2＋2eq \r(x)＋1－1＝(eq \r(x)＋1)2－1，且eq \r(x)＋1≥1.∴f(x)＝x2－1(x≥1)．
解法二(换元法) 设t＝eq \r(x)＋1，则x＝(t－1)2(t≥1)．代入原式有f(t)＝(t－1)2＋2(t－1)＝t2－2t＋1＋2t－2＝t2－1.
故f(x)＝x2－1(x≥1)．
答案：f(x)＝x2－1(x≥1)
2．解析：设f(x)＝ax＋b(a≠0)，则f(f(x))＝af(x)＋b＝a2x＋ab＋b＝4x＋3，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(a2＝4，,ab＋b＝3，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝2，,b＝1))或eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝－2，,b＝－3，))
∴f(x)＝2x＋1或f(x)＝－2x－3.
答案：f(x)＝2x＋1或f(x)＝－2x－3
3．解析：因为2f(x)＋feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)))＝3x，①
所以将x用eq \f(1,x)替换，得2feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)))＋f(x)＝eq \f(3,x)，②
由①②解得f(x)＝2x－eq \f(1,x)(x≠0)，
即f(x)的解析式是f(x)＝2x－eq \f(1,x)(x≠0)．
答案：2x－eq \f(1,x)(x≠0)
考点三
例2 解析：(1)因为f(1)＝12＋2＝3，所以f(f(1))＝f(3)＝3＋eq \f(1,3－2)＝4.故选C.
(2)当m≥2时，m2－1＝3，所以m＝2或m＝－2(舍)；
当0所以m＝2.所以feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)－m))＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))＝lg2eq \f(1,2)＝－1.
答案：(1)C (2)－1
例3 解析：(1)因为eq \f(2,3)＜1，所以feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)))＝4×eq \f(2,3)＋a＝a＋eq \f(8,3).
若a＋eq \f(8,3)≥1，即a≥－eq \f(5,3)时，＝4，
即a＋eq \f(8,3)＝2⇒a＝－eq \f(2,3)＞－eq \f(5,3)(成立)；
若a＋eq \f(8,3)＜1，即a＜－eq \f(5,3)时，则4a＋eq \f(32,3)＋a＝4，
即a＝－eq \f(4,3)＞－eq \f(5,3)(舍去)，综上a＝－eq \f(2,3).
(2)将函数f(x)的图象画出来，观察图象可知eq \b\lc\{\rc\ (\a\vs4\al\c1(2x＜0，,2x＜x＋1，))解得x＜0，所以满足f(x＋1)＜f(2x)的x的取值范围是(－∞，0)．故选D.
答案：(1)A (2)D
同类练
4．解析：因为f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x，x<0,ex－1，x≥0))，所以f(2)＋f(－1)＝e2－1－1＝e2－2.
答案：e2－2
5．解析：f(1)＝12－3×1－3＝－5，f(－5)＝2×(－5)＋12＝2，故选D.
答案：D
变式练
6．解析：f(－4)＝16－4－2＝10，所以f(f(－4))＝f(10)＝1－lg 10＝0.
答案：0
7．解析：解法一 当01.
所以f(a)＝eq \r(a)，f(a＋1)＝2(a＋1－1)＝2a.
由f(a)＝f(a＋1)得eq \r(a)＝2a，
所以a＝eq \f(1,4).
此时feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a)))＝f(4)＝2×(4－1)＝6.
当a≥1时，a＋1>1，
所以f(a)＝2(a－1)，f(a＋1)＝2(a＋1－1)＝2a.
由f(a)＝f(a＋1)得2(a－1)＝2a，无解．
综上，feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a)))＝6，故选C.
解法二 因为当0当x≥1时，f(x)＝2(x－1)，为增函数，
又f(a)＝f(a＋1)，所以eq \r(a)＝2(a＋1－1)，
所以a＝eq \f(1,4).
所以feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a)))＝f(4)＝6.
答案：C
拓展练
8．解析：当x≥0时，f(x)＝eq \f(x,2)≥0，
所以f(f(x))＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,2)))＝eq \f(x,4)≥1，解得x≥4；
当x<0时，f(x)＝x2>0，
所以f(f(x))＝f(x2)＝eq \f(x2,2)≥1，解得x≥eq \r(2)(舍)或x≤－eq \r(2).
综上，f(f(x))≥1的解集为(－∞，－eq \r(2)]∪[4，＋∞)．故选D.
答案： D函数
映射
两集合A，B
A，B是两个非空数集
A，B是两个①________
对应关系
f：A→B
按照某种确定的对应关系f，对于集合A中的②________一个数x，在集合B中有③________的数f(x)和它对应
按某一个确定的对应关系f，对于集合A中的④________一个元素x，在集合B中都有⑤________的元素y与之对应
名称
那么就称f：A→B为从集合A到集合B的一个函数
那么就称对应f：A→B为从集合A到集合B的一个映射
记法
y＝f(x)，x∈A
对应f：A→B是一个映射