2022年中考数学专题复习类型七 二次函数与直角三角形有关的问题（原卷版）

类型七 二次函数与直角三角形有关的问题

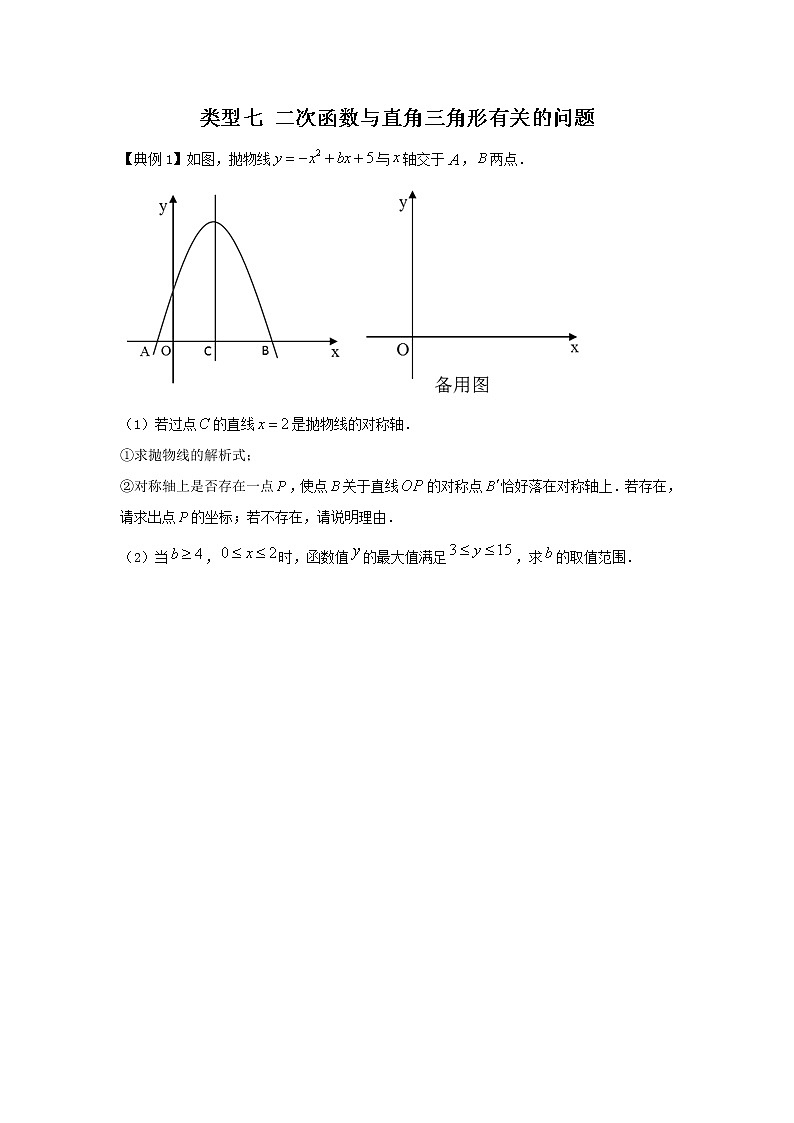
【典例1】如图，抛物线与轴交于，两点．

（1）若过点的直线是抛物线的对称轴．

①求抛物线的解析式；

②对称轴上是否存在一点，使点关于直线的对称点恰好落在对称轴上．若存在，请求出点的坐标；若不存在，请说明理由．

（2）当，时，函数值的最大值满足，求的取值范围．

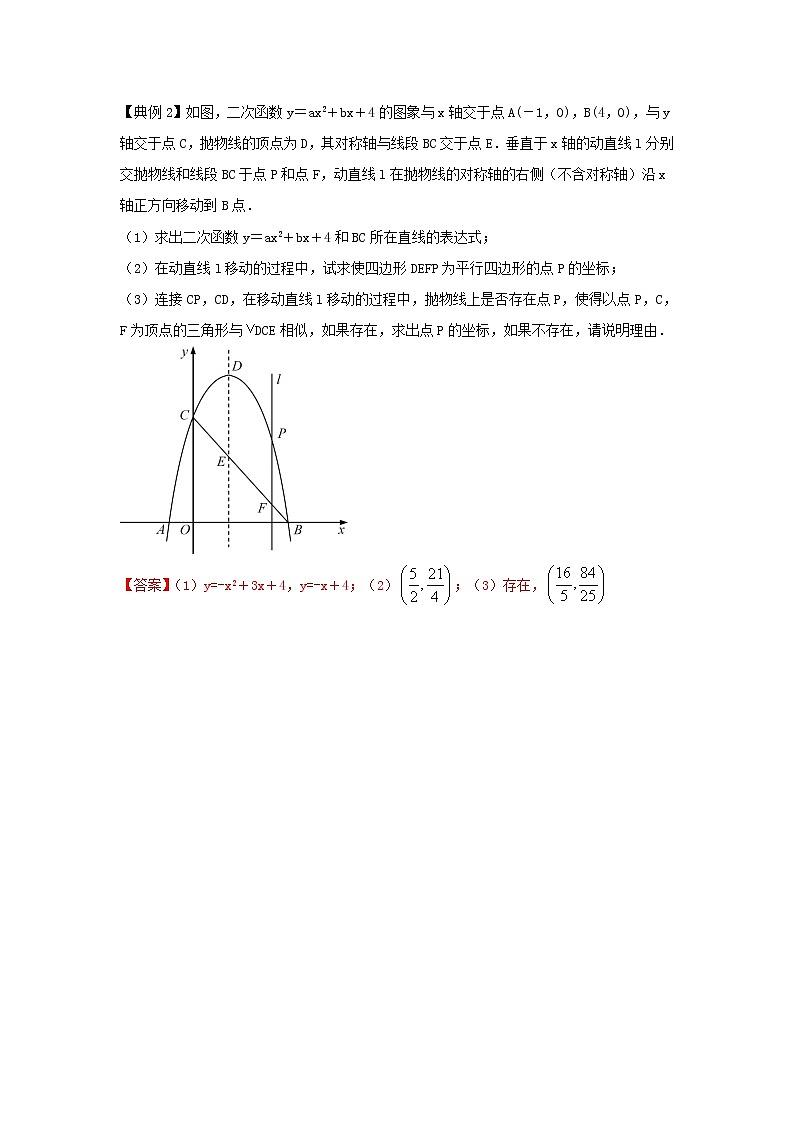
【典例2】如图，二次函数y＝ax2＋bx＋4的图象与x轴交于点A(－1，0)，B(4，0)，与y轴交于点C，抛物线的顶点为D，其对称轴与线段BC交于点E．垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F，动直线l在抛物线的对称轴的右侧（不含对称轴）沿x轴正方向移动到B点．

（1）求出二次函数y＝ax2＋bx＋4和BC所在直线的表达式；

（2）在动直线l移动的过程中，试求使四边形DEFP为平行四边形的点P的坐标；

（3）连接CP，CD，在移动直线l移动的过程中，抛物线上是否存在点P，使得以点P，C，F为顶点的三角形与DCE相似，如果存在，求出点P的坐标，如果不存在，请说明理由．

【答案】（1）y=-x2＋3x＋4，y=-x＋4；（2）；（3）存在，

【典例3】如图，抛物线与轴交于，两点（点在点的左侧），与轴交于点．直线与抛物线交于，两点，与轴交于点，点的坐标为．

（1）请直接写出，两点的坐标及直线的函数表达式；

（2）若点是抛物线上的点，点的横坐标为，过点作轴，垂足为．与直线交于点，当点是线段的三等分点时，求点的坐标；

（3）若点是轴上的点，且，求点的坐标．

【典例4】如图1，排球场长为18m，宽为9m，网高为2.24m．队员站在底线O点处发球，球从点O的正上方1.9m的C点发出，运动路线是抛物线的一部分，当球运动到最高点A时，高度为2.88m．即BA＝2.88m．这时水平距离OB＝7m，以直线OB为x轴，直线OC为y轴，建立平面直角坐标系，如图2．

（1）若球向正前方运动（即x轴垂直于底线），求球运动的高度y（m）与水平距离x（m）之间的函数关系式（不必写出x取值范围）．并判断这次发球能否过网？是否出界？说明理由；

（2）若球过网后的落点是对方场地①号位内的点P（如图1，点P距底线1m，边线0.5m），问发球点O在底线上的哪个位置？（参考数据：取1.4）