2020-2021年江西省赣州市高二（上）期末考试数学试卷北师大版

这是一份2020-2021年江西省赣州市高二（上）期末考试数学试卷北师大版，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 已知命题p：对任意x>1，有xlnx>x−1成立，则¬p为( )
A.存在x0≤1，使x0lnx0≤x0−1成立
B.存在x0>1，使x0lnx0≤x0−1成立
C.对任意x0≤1，有x0lnx0≤x0−1成立
D.对任意x0>1，有x0lnx0≤x0−1成立

2. 已知椭圆x216+y2m2=1的右焦点为2,0，则m=( )
A.23B.25C.±23D.±25

3. 若l，m是两条不同的直线，m垂直于平面α，则“l⊥m”是“l // α”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件

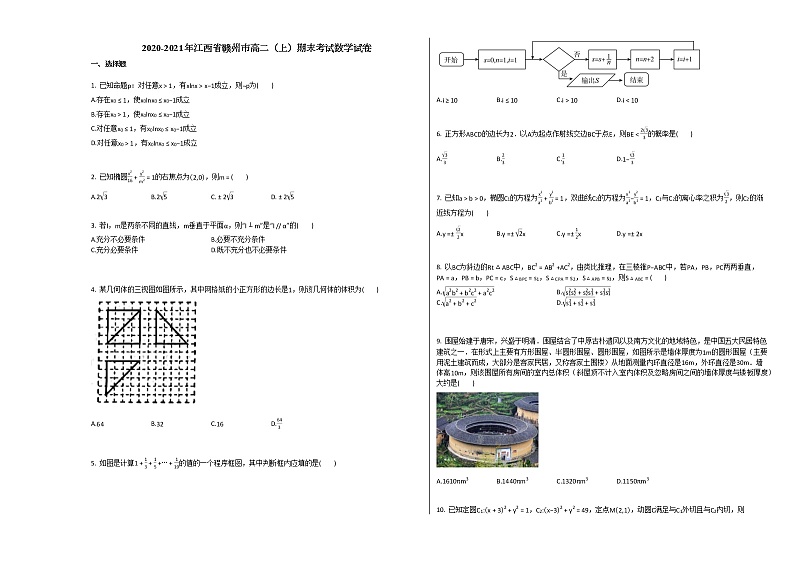
4. 某几何体的三视图如图所示，其中网格纸的小正方形的边长是1，则该几何体的体积为( )

A.64 B.32C.16D.643

5. 如图是计算1+13+15+⋯+119的值的一个程序框图，其中判断框内应填的是( )

A.i≥10B.i≤10C.i>10D.i<10

6. 正方形ABCD的边长为2．以A为起点作射线交边BC于点E，则BE<233的概率是( )
A.33B.23C.13D.1−33

7. 已知a>b>0，椭圆C1的方程为x2a2+y2b2=1，双曲线C2的方程为x2a2−y2b2=1，C1与C2的离心率之积为32，则C2的渐近线方程为( )
A.y=±22xB.y=±2xC.y=±12xD.y=±2x

8. 以BC为斜边的Rt△ABC中，BC2=AB2+AC2，由类比推理，在三棱锥P−ABC中，若PA，PB，PC两两垂直，PA=a，PB=b，PC=c，S△BPC=s1，S△CPA=s2，S△APB=s3，则S△ABC=( )
A.a2b2+b2c2+a2c2B.s12s22+s22s32+s32s12
C.a2+b2+c2D.s12+s22+s32

9. 围屋始建于唐宋，兴盛于明清．围屋结合了中原古朴遗风以及南方文化的地域特色，是中国五大民居特色建筑之一．在形式上主要有方形围屋、半圆形围屋、圆形围屋，如图所示是墙体厚度为1m的圆形围屋（主要用泥土建筑而成，大部分是客家民居，又称客家土围楼）从地面测量内环直径是16m，外环直径是30m．墙体高10m，则该围屋所有房间的室内总体积（斜屋顶不计入室内体积及忽略房间之间的墙体厚度与矮板厚度）大约是( )

A.1610πm3B.1440πm3C.1320πm3D.1150πm3

10. 已知定圆C1:x+32+y2=1，C2:x−32+y2=49，定点M2,1，动圆C满足与C1外切且与C2内切，则|CM|+|CC1|的最大值为( )
A.8+2B.8−2C.16+2D.16−2

11. 如图，已知棱长为2的正方体ABCD−A1B1C1D1中，点G是B1C的中点，点H，E分别为GD，C1D的中点．GD⊥平面α，HE⫋平面α，△A1C1D与平面α相交于一条线段，则该线段的长度是( )

A.144B.114C.142D.112

12. 设直线l与圆x−22+y2=3相切于N，与抛物线y2=2pxp>0交于A，B两点，且N是线段AB的中点，若直线l有且只有4条，则p的取值范围是( )
A.1,3B.1,3C.0,3D.0,3
二、填空题

已知抛物线y=2x2，则其准线方程为________.

下面是两个变量的一组数据：
这两个变量之间的线性回归方程为y=−15+9x，变量y中缺失的数据是________.

在边长为3的菱形ABCD中，对角线AC=3，将△ABC沿AC折起，使得二面角B−AC−D的大小为π2，则三棱锥B−ACD外接球的体积是________.

已知双曲线C:x2a2−y2b2=1a>0,b>0右支上一点P，F1，F2分别为其左右焦点，圆M是△PF1F2内切圆，且PF1与圆M相切于点A，|PA|=c22a （c为半焦距），若|PF1||PF2|>2，则双曲线离心率的取值范围是________.
三、解答题

已知p：方程x2m−1+y2m−4=1表示双曲线，q：方程x2m+2+y26−m=1表示焦点在x轴上的椭圆．
(1)若“p且q”为真命题，求实数m的取值范围；

(2)若“p且q”是假命题，“p或q​”为真命题，求实数m的取值范围．

1971年，江西省赣州地区信丰县开辟脐橙种植实验基地，1975年11月，出自此基地的脐橙参加赣南农产品大比武大放异彩，1976年广交会上脐橙“一炮打响”，1977年脐橙销往香港市场，1980年中科院考察队认定赣南是得天独厚的柑橘生产地，时至今日赣南脐橙已享誉全球．据市场反馈“腰围”长是25cm∼27cm的脐橙最受消费者青睐，某种植户在甲、乙两块地种植脐橙，从两种植地采摘的脐橙中分别随机抽取100颗脐橙（“腰围”长均在21cm∼31cm），根据“腰围”长分类画出如下统计图表：

(1)求乙种植地脐橙腰围长的中位数；

(2)从甲种植地样本在23cm∼25cm，25cm∼27cm两段中用分层抽样的方法抽出6颗脐橙，某同学随机的从6颗中拿走2颗，问拿到的2颗都是受消费者青睐的概率是多少？

在三棱锥P−ABC中，AE⊥BC于点E，CF⊥AB于点F，且AE∩CF=O ，若点P在平面ABC上的射影为点O．

(1)证明：AC⊥PB；

(2)若△ABC是正三角形，点G，H分别为PA，PC的中点．证明：四边形EFGH是矩形.

已知动圆与直线x=−1相交于A，B两点，且|AB|=23.
(1)当动圆过定点2,0时，求动圆圆心C的轨迹方程；

(2)过点−1,0的直线l交(1)中动圆圆心C的轨迹于M，N两点，点P为M，N的中点，过点P垂直于直线l的直线交x轴于点Q，求点Q的横坐标的取值范围．

如图，已知三棱柱ABC−A1B1C1的所有棱长均为2，∠B1BA=π3.

(1)证明：B1C⊥平面ABC1 ；

(2)若平面ABB1A1⊥平面ABC，M为A1C1的中点，求二面角C−AB1−M的余弦值．

已知椭圆C:x2a2+y2b2=1的左右顶点分别为A1−2,0，A22,0．椭圆C上不同于A1，A2的任意一点P，直线PA1和PA2的斜率之积为−34.

(1)求椭圆C的标准方程；

(2)过椭圆内一点Mm,0m≠0．作一条不垂直于x轴的直线交椭圆于A，B两点，点Q和点B关于x轴对称，直线AQ交x轴于点Nn,0，证明： m⋅n为定值．
参考答案与试题解析
2020-2021年江西省赣州市高二（上）期末考试数学试卷
一、选择题
1.
【答案】
B
【考点】
命题的否定
【解析】
利用全称命题的否定为特称命题，进行求解即可.
【解答】
解：全称命题的否定为特称命题.
因为命题p：对任意x>1，有xlnx>x−1成立，
所以¬p：存在x0>1，使x0lnx0≤x0−1成立.
故选B.
2.
【答案】
C
【考点】
椭圆的标准方程
【解析】
由题意可知该椭圆的焦点在x轴上，且c=2，由c2=16−m2=4，解方程即可.
【解答】
解：∵椭圆x216+y2m2=1的右焦点为2,0，
∴ c2=16−m2=4，
解得m=±23.
故选C.
3.
【答案】
B
【考点】
充分条件、必要条件、充要条件
【解析】
利用直线与平面平行与垂直关系，判断两个命题的充要条件关系即可．
【解答】
解：∵l，m是两条不同的直线，m垂直于平面α，
若“l⊥m”，
则“l // α”或l⊂α，故充分性不成立；
反之，“l // α”一定有“l⊥m”，故必要性成立，
∴“l⊥m”是“l // α”的必要不充分条件．
故选B.
4.
【答案】
D
【考点】
由三视图求体积
【解析】
还原几何体，由棱锥的体积进行求解即可.
【解答】
解：还原几何体如图中A−BCDE所示：
其中几何体A−BCDE是以高为4，底面边长为4的正方形的四棱锥，
故该几何体的体积为13×4×4×4=643.
故选D.
5.
【答案】
C
【考点】
程序框图
循环结构的应用
【解析】
分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S的值．
【解答】
解：程序运行过程中，各变量值如下表所示：
第一次循环：S=1，n=3，i=2；
第二次循环：S=1+13，n=5，i=3；
第三次循环：S=1+13+15，n=7，i=4，
⋯，
第十次循环：S=S=1+13+15+…+119，n=21，i=11退出循环.
其中判断框内应填入的条件是：i>10.
故选C．
6.
【答案】
B
【考点】
几何概型计算（与长度、角度、面积、体积有关的几何概型）
【解析】
首先根据题意，画出几何图形，然后求出概率．
【解答】
解：如图，作正方形ABCD，
在△ABE中，令BE=233，
∵AB=2，
∴tanθ=BEAB=33，
∴ θ=π6，
∴ 当0<θ<π6时，BE<233.
∵以A为射线BC相交，
∴总的基本事件是θ取到最大角即∠CAB=π4，
∴ BE<233的概率P=π6π4=46=23.
故选B.
7.
【答案】
A
【考点】
双曲线的离心率
双曲线的渐近线
椭圆的离心率
【解析】
求出椭圆与双曲线的离心率，根据离心率之积的关系，然后推出a，b关系，即可求解双曲线的渐近线方程．
【解答】
解：∵a>b>0，椭圆C1的方程为x2a2+y2b2=1，
∴C1的离心率e1=a2−b2a.
∵双曲线C2的方程为x2a2−y2b2=1，
∴C2的离心率为e2=a2+b2a.
∵ e1⋅e2=32，
∴ a2−b2a⋅a2+b2a=32，
∴ (ba)2=12，
∴ba=22，
∴C2的渐近线方程为y=±22x.
故选A.
8.
【答案】
D
【考点】
类比推理
【解析】
此题暂无解析
【解答】
解：由题意可知 PA，PB，PC两两垂直
∴ S△BPC，S△APB，S△CPA 类比于AB与AC，S△ABC 类比于BC，
∴S△ABC=s12+s22+s32.
故选D．
9.
【答案】
D
【考点】
柱体、锥体、台体的体积计算
【解析】
由圆柱体积公式计算即可.
【解答】
解：由题意可得总体积为：
V=π×302−12×10−π×162+12×10
=1150πm3.
故选D.
10.
【答案】
A
【考点】
圆与圆的位置关系及其判定
椭圆的定义
椭圆的应用
【解析】
先根据题意得动圆C的圆心的轨迹是一个椭圆，其中C1，C2为焦点，再进一步去判断M2,1在椭圆内，再由此去求CM+CC1的最大值.
【解答】
解：由题意得圆C1的圆心为C1−3,0，半径为1，
圆C2的圆心为C23,0，半径为7，
设动圆C半径为r，
则CC1=r+1，CC2=7−r，
则CC1+CC2=8.
∵C1C2=−3−32+0−02=6，
∴CC1+CC2>C1C2，
∴圆心C的轨迹是一个椭圆，其中C1，C2为焦点，
∴2a=8，2c=6，
∴b2=42−32=7，
即椭圆方程为x216+y27=1.
∵2216+127=1128<1，
∴M2,1在椭圆内，
∴CM+CC1=CM+8−CC2≤8+MC2.
∵MC2=2−32+1−02=2，
∴CM+CC1的最大值为8+2.
故选A.
11.
【答案】
C
【考点】
点到直线的距离公式
点、线、面间的距离计算
【解析】
此题暂无解析
【解答】
解：以A为坐标原点，以AB，AD，AA1分别为x，y，z轴建立如图所示的空间直角坐标系，
则A0,0,0，B2,0,0，C2,2,0，D0,2,0，
A10,0,2，B12,0,2，C12,2,2，D10,2,2，
G(2,1,1)，H(1,32,12)，E(1,2,1)，
∴DG→=(2,−1,1)，
∵GD⊥平面α，
∴DG→=(2,−1,1)为平面α的法向量，
∴平面α的解析式为2x−y+z=0，
代入平面上点H，
得2x−y+z=2xH−yH+zH=2−32+12=1，
∴△A1C1D的边C1D与平面α交于E(1,2,1)，
△A1C1D的边A1D与平面α交于F，设F(0,a,2−a)，
代入平面α，2×0−a+(2−a)=1，
解得a=12，
∴F(0,12,32)，
∴线段EF的长度：12+(2−12)2+(1−32)2=142.
故选C．
12.
【答案】
B
【考点】
抛物线的求解
直线与圆的位置关系
抛物线的性质
【解析】
此题暂无解析
【解答】
解：设Ax1,y1，Bx2,y2，Nx0,y0，直线l的斜率为k，
因为l有且仅有四条，
当斜率不存在时有x=2±3两种情况；
所以当斜率不存在时有两条.
因为点A，B在y2=2px上，
所以y12=2px1，y22=2px2，
两式相减得y1−y2y1+y2=2px1−x2.
因为N是线段AB的中点，
所以 y1+y2=2y0，
此时y1−y2x1−x2=2py1+y2，
所以y0k=p.
因为l与圆(x−2)2+y2=3相切于点N，
所以y0x0−2=−1k，
即x0−2=−y0k=−p ，
解得x0=2−p ，
将x0=2−p代入y2=2px得y2=2p2−p，
所以y0<2p2−p，
因为点N在圆(x−2)2+y2=3上，
所以x0−22+y02=3，
即y02=3−p2，
所以3−p2<2p2−p ，
整理得p2−4p+3<0，
解得1所以p的取值范围为(1,3).
故选B.
二、填空题
【答案】
y=−18
【考点】
抛物线的标准方程
抛物线的性质
【解析】
将抛物线方程化为x2=12y，可得到准线方程．
【解答】
解：∵y=2x2，
∴x2=12y，
∴2p=12，
∴p2=18.
∵抛物线方程开口向上，
∴准线方程是y=−18.
故答案为：y=−18．
【答案】
4
【考点】
众数、中位数、平均数
回归分析的初步应用
求解线性回归方程
【解析】
求出x¯，y¯，然后将x¯，y¯代入回归方程，得出关于m的关系式，便可得出结果.
【解答】
解：∵ x¯=1+2+3+4+5+6+7+88=368，
设缺失的数据是m，
则y¯=1+m+9+16+25+36+49+648=200+m8.
因为线性回归方程y=−15+9x一定过样本中心点(x¯,y¯)，
所以将x¯，y¯代入y=−15+9x，得200+m8=−15+9×368，
解得m=4.
故答案为4.
【答案】
55π6
【考点】
球内接多面体
【解析】
此题暂无解析
【解答】
解：设△ABC外心为O1，△ACD外心为O2，
过O1作平面ABC的垂线，过O2作平面ACD的垂线，两垂线交点O即为外接球球心，取AC中点E，如图，
∵ BA=BC，
∴ BE⊥AC，
同理DE⊥AC，
∴ ∠BED为二面角B−AC−D的平面角.
∵二面角B−AC−D大小为π2，
∴∠BED=π2，
∴BE⊥平面ACD.
又∵OO2⊥平面ACD，
∴BE//OO2，
同理DE//OO1.
又∵ ∠BED=π2，
∴ 四边形OO1EO2为矩形.
在等边三角形ABC中，∵O1为外心，
∴O1为重心，
∴O1E=13BE=13BC⋅cs30∘=12，
同理O2E=12，
∴矩形 OO1EO2 为正方形 ，
∴OO1=O1E=12.
∵OO1⊥ 平面ABC，BE⊂平面ABC，
∴OO1⊥BE.
在Rt△OO1B中，∵OO1=12，O1B=2O1E=1，
∴外接球的半径R=OB=OO12+O1B2=52，
∴V=43πR3=55π6．
故答案为： 55π6.
【答案】
1,7−1
【考点】
双曲线的离心率
双曲线的标准方程
【解析】
由圆的切线的性质求得|PF1|,PF2,再利用PF1PF2>2,得到a,c的不等式，即可求得离心率的取值范围.
【解答】
解：由题可得示意图如图，
∴F1N=a+c，F2N=c−a，
∴PF1=a+c+c22a，
∵|PF1|−|PF2|=2a，
∴PF2=c−a+c22a.
∵PF1PF2>2，
∴a+c+c22ac−a+c22a>2，
整理得e2+2e−6<0，
即−1−7又∵e>1，
∴1∴e的取值范围是1,7−1.
故答案为：1,7−1.
三、解答题
【答案】
解：(1)因为"p且q"为真命题，
所以p，q是真命题.
因为p是真命题，所以m−1m−4<0，
解得1因为q是真命题，所以m+2>6−m>0，
解得2综上2(2)当p真q假时，有1解得1若p假q真时，有m≤1或m≥4，2解得4≤m<6.
所以1【考点】
椭圆的标准方程
双曲线的标准方程
圆锥曲线的综合问题
逻辑联结词“或”“且”“非”
【解析】
此题暂无解析
【解答】
解：(1)因为"p且q"为真命题，
所以p，q是真命题.
因为p是真命题，所以m−1m−4<0，
解得1因为q是真命题，所以m+2>6−m>0，
解得2综上2(2)当p真q假时，有1解得1若p假q真时，m≤1或m≥4，2解得4≤m<6.
所以1【答案】
解：(1)x¯甲=22×0.1+24×0.2+26×0.4+28×0.15+
30×0.15=26.1；
x¯乙=22×0.1+24×0.2+26×0.3+28×0.3+30×0.1=26.2，
设乙种植地的中位数为x，
则x−25×0.15=0.2，
解得x=793.
(2)由频率分布直方图可知甲地23cm∼25cm的脐橙个数为0.2×100=20个,
抽出110×20=2个，假设为Q1，Q2.
25cm∼27cm的脐橙个数为0.4×100=40个.
抽出110×40=4个，假设为C1，C2，C3，C4.
从这6颗中抽出2颗可能产生的结果为：
Q1Q2，Q1C1，Q1C2，Q1C3，Q1C4，Q2C1，Q2C2，Q2C3，Q2C4，C1C2，C1C3，C1C4，C2C3，C2C4，C3C4，共15种．
2颗都是受消费者青睐的包括：
C1C2，C1C3，C1C4，C2C3，C2C4，C3C4共6种，
所以2颗都受消费者青睐的概率P=615=25.
【考点】
众数、中位数、平均数
列举法计算基本事件数及事件发生的概率
【解析】
此题暂无解析
【解答】
解：（1）x¯甲=22×0.1+24×0.2+26×0.4+28×0.15+
30×0.15=26.1；
x¯乙=22×0.1+24×0.2+26×0.3+28×0.3+30×0.1=26.2
设乙种植地的中位数为x，则x−25×0.15=0.2，
解得x=793.
(2)由频率分布直方图可知甲地23cm∼25cm的脐橙个数为0.2×100=20个,
抽出110×20=2个，假设为Q1，Q2.
25cm∼27cm的脐橙个数为0.4×100=40个.
抽出110×40=4个，假设为C1，C2，C3，C4.
从这6颗中抽出2颗可能产生的结果为：
Q1Q2，Q1C1，Q1C2，Q1C3，Q1C4，Q2C1，Q2C2，Q2C3，Q2C4，C1C2，C1C3，C1C4，C2C3，C2C4，C3C4，共15种．
2颗都是受消费者青睐的包括：
C1C2，C1C3，C1C4，C2C3，C2C4，C3C4共6种，
所以2颗都受消费者青睐的概率P=615=25.
【答案】
证明：(1)连接BO并延长交AC于点M，如图．
因为AE⊥BC，CF⊥AB，
所以O为△ABC的垂心，
所以BM⊥AC.
因为P在平面ABC的射影为O，
所以PO⊥平面ABC，
所以PO⊥AC.
又因为PO∩BM=O，
所以AC⊥平面PBM，
所以AC⊥PB.
(2)因为AE⊥BC，CF⊥AB，△ABC为正三角形，
所以E，F分别为BC，BA的中点，
所以EF//AC.
由(1)知AC⊥PB，所以EF⊥PB.
因为E，H分别为BC，PC的中点，
所以EH=//12PB.
又因为F，G分别为AB，PA的中点，
所以GF=//12PB，
所以EH=//GF，
所以四边形EFGH为平行四边形.
又因为EH//PB，EF⊥PB，
所以EH⊥EF，
所以四边形EFGH为矩形.
【考点】
两条直线垂直的判定
【解析】
此题暂无解析
【解答】
证明：(1)连接BO并延长交AC于点M，如图．
因为AE⊥BC，CF⊥AB，
所以O为△ABC的垂心，
所以BM⊥AC.
因为P在平面ABC的射影为O，
所以PO⊥平面ABC，
所以PO⊥AC.
又因为PO∩BM=O，
所以AC⊥平面PBM，
所以AC⊥PB.
(2)因为AE⊥BC，CF⊥AB，△ABC为正三角形，
所以E，F分别为BC，BA的中点，
所以EF//AC.
由(1)知AC⊥PB，所以EF⊥PB.
因为E，H分别为BC，PC的中点，
所以EH=//12PB.
又因为F，G分别为AB，PA的中点，
所以GF=//12PB，
所以EH=//GF，
所以四边形EFGH为平行四边形.
又因为EH//PB，EF⊥PB，
所以EH⊥EF，
所以四边形EFGH为矩形.
【答案】
解：(1)设Cx,y，
则x+12+3=x−22+y2，
整理得y2=6x，
所以圆心C的轨迹方程为y2=6x.
(2)设过点−1,0直线MN为y=kx+1，
联立y2=6x，y=kx+1，
消去y得k2x2+2k2−6x+k2=0，
所以Δ=2k2−62−4k4>0，即k2<32.
设Mx1,y1，Nx2,y2，
所以 x1+x2=6k2−2，x1x2=1,
所以MN的中点P3k2−1,3k，
过点P的垂线为y−3k=−1kx−3k2−1,
令y=0，则x=3k2+2>4，
所以点Q的横坐标的取值范围4,+∞.
【考点】
轨迹方程
直线与圆的位置关系
与抛物线有关的中点弦及弦长问题
【解析】
此题暂无解析
【解答】
解：(1)设Cx,y，则x+12+3=x−22+y2，
整理得y2=6x，
所以圆心C的轨迹方程为y2=6x.
(2)设过点−1,0直线MN为y=kx+1，
联立y2=6x，y=kx+1，
消去y得k2x2+2k2−6x+k2=0，
所以Δ=2k2−62−4k4>0，即k2<32.
设Mx1,y1，Nx2,y2，
所以 x1+x2=6k2−2，x1x2=1,
所以MN的中点P3k2−1,3k，
过点P的垂线为y−3k=−1kx−3k2−1,
令y=0，则x=3k2+2>4，
所以点Q的横坐标的取值范围4,+∞.
【答案】
(1)证明：如图取AB中点D，连结B1D，CD，
因为四边形BCC1B1为菱形，
所以B1C⊥BC1.
又因为三棱柱的所有棱长均为2，∠B1BA=π3，
所以△ABC和△ABB1是等边三角形，
所以B1D⊥AB，CD⊥AB.
因为B1D，CD⊂平面B1CD，B1D∩CD=D，
所以AB⊥平面B1CD，
所以B1C⊥AB，又BC1∩AB=B，
所以B1C⊥平面ABC1.
(2)解：因为平面ABB1A1⊥平面ABC，且交线为AB，
由(2)知B1D⊥AB，
所以B1D⊥平面ABC，
所以DB，DB1，DC两两垂直，
以D为原点，DB为x轴，DC为y轴，DB1为z轴，建立如图所示的空间直角坐标系．
则D(0,0,0)，A(−1,0,0)，B1(0,0,3)，C(0,3,0)，
C1(−1,3,3)，A1(−2,0,3)，
因为M为A1C1的中点，所以M−32,32,3，
所以AC→=(1,3,0)，AB1→=(1,0,3)，AM→=(−12,32,3)，
设平面AB1M的法向量为n1→=(x1,y1,z1)，
则AB1→⋅n1→=x1+3z1=0，AM→⋅n1→=−12x1+32y1+3z1=0，
取z1=1，得n1→=(−3,−3,1).
设平面AB1C的法向量为n2→=(x2,y2,z2)，
则AB1→⋅n2→=x2+3z2=0，AC→⋅n2→=x2+3y2=0，
取z2=1，得n2→=(−3,1,1)，
所以cs=n1→⋅n2→|n1→||n2→|=113×5=6565，
所以所求二面角C−AB1−M的余弦值为6565.
【考点】
直线与平面垂直的判定
用空间向量求平面间的夹角
【解析】
此题暂无解析
【解答】
(1)证明：如图取AB中点D，连结B1D，CD，
因为四边形BCC1B1为菱形，
所以B1C⊥BC1.
又因为三棱柱的所有棱长均为2，∠B1BA=π3，
所以△ABC和△ABB1是等边三角形，
所以B1D⊥AB，CD⊥AB.
因为B1D，CD⊂平面B1CD，B1D∩CD=D，
所以AB⊥平面B1CD，
所以B1C⊥AB，又BC1∩AB=B，
所以B1C⊥平面ABC1.
(2)解：因为平面ABB1A1⊥平面ABC，且交线为AB，
由(2)知B1D⊥AB，
所以B1D⊥平面ABC，
所以DB，DB1，DC两两垂直，
以D为原点，DB为x轴，DC为y轴，DB1为z轴，建立如图所示的空间直角坐标系．
则D(0,0,0)，A(−1,0,0)，B1(0,0,3)，C(0,3,0)，
C1(−1,3,3)，A1(−2,0,3)，
因为M为A1C1的中点，所以M−32,32,3，
所以AC→=(1,3,0)，AB1→=(1,0,3)，AM→=(−12,32,3)，
设平面AB1M的法向量为n1→=(x1,y1,z1)，
则AB1→⋅n1→=x1+3z1=0，AM→⋅n1→=−12x1+32y1+3z1=0，
取z1=1，得n1→=(−3,−3,1).
设平面AB1C的法向量为n2→=(x2,y2,z2)，
则AB1→⋅n2→=x2+3z2=0，AC→⋅n2→=x2+3y2=0，
取z2=1，得n2→=(−3,1,1)，
所以cs=n1→⋅n2→|n1→||n2→|=113×5=6565，
所以所求二面角C−AB1−M的余弦值为6565.
【答案】
(1)解：由题可知a=2，
令P0,b，
所以kPA1⋅kPA2=b2−4=−34，
所以b2=3，
所以椭圆C的标准方程为x24+y23=1.
(2)证明：显然直线AB的斜率存在，设直线AB的方程为y=kx−m，
联立3x2+4y2=12，y=kx−m，
消y得3+4k2x2−8mk2x+4k2m2−12=0，
设Ax1,y1，Bx2,y2，则Qx2,−y2，
所以x1+x2=8mk23+4k2，x1x2=4k2m2−123+4k2，
所以直线AQ:y−y1=y1+y2x1−x2x−x1，
令y=0，
则n=x=−y1x1−x2y1+y2+x1
=y1x2+x1y2y1+y2=kx1−mx2+kx2−mx1kx1−m+kx2−m
=2x1x2−mx1+x2x1+x2−2m=2×4k2m2−123+4k2−m×8mk23+4k28mk23+4k2−2m
=24m2k2−12−8m2k28mk2−6m−8mk2=−24−6m=4m，
所以m⋅n=m⋅4m=4，为定值.
【考点】
椭圆的标准方程
圆锥曲线中的定点与定值问题
【解析】
此题暂无解析
【解答】
(1)解：由题可知a=2，
令P0,b，
所以kPA1⋅kPA2=b2−4=−34，
所以b2=3，
所以椭圆C的标准方程为x24+y23=1.
(2)证明：显然直线AB的斜率存在，设直线AB的方程为y=kx−m，
联立3x2+4y2=12，y=kx−m，
消y得3+4k2x2−8mk2x+4k2m2−12=0，
设Ax1,y1，Bx2,y2，Qx2,−y2，
所以x1+x2=8mk23+4k2，x1x2=4k2m2−123+4k2，
所以直线AQ:y−y1=y1+y2x1−x2x−x1，
令y=0，则n=x=−y1x1−x2y1+y2+x1
=y1x2+x1y2y1+y2=kx1−mx2+kx2−mx1kx1−m+kx2−m
=2x1x2−mx1+x2x1+x2−2m=24k2m2−123+4k2−m8mk23+4k28mk23+4k2−2m
=24m2k2−12−8m2k28mk2−6m−8mk2=−24−6m=4m，
所以m⋅n=m⋅4m=4，为定值.x
1
2
3
4
5
6
7
8
y
1
9
16
25
36
49
64