第1章 第3节　全称量词命题与存在量词命题-2022届高三数学一轮复习讲义（新高考）教案

这是一份第1章 第3节　全称量词命题与存在量词命题-2022届高三数学一轮复习讲义（新高考）教案，共5页。教案主要包含了教材概念·结论·性质重现，基本技能·思想·活动体验等内容，欢迎下载使用。
一、教材概念·结论·性质重现
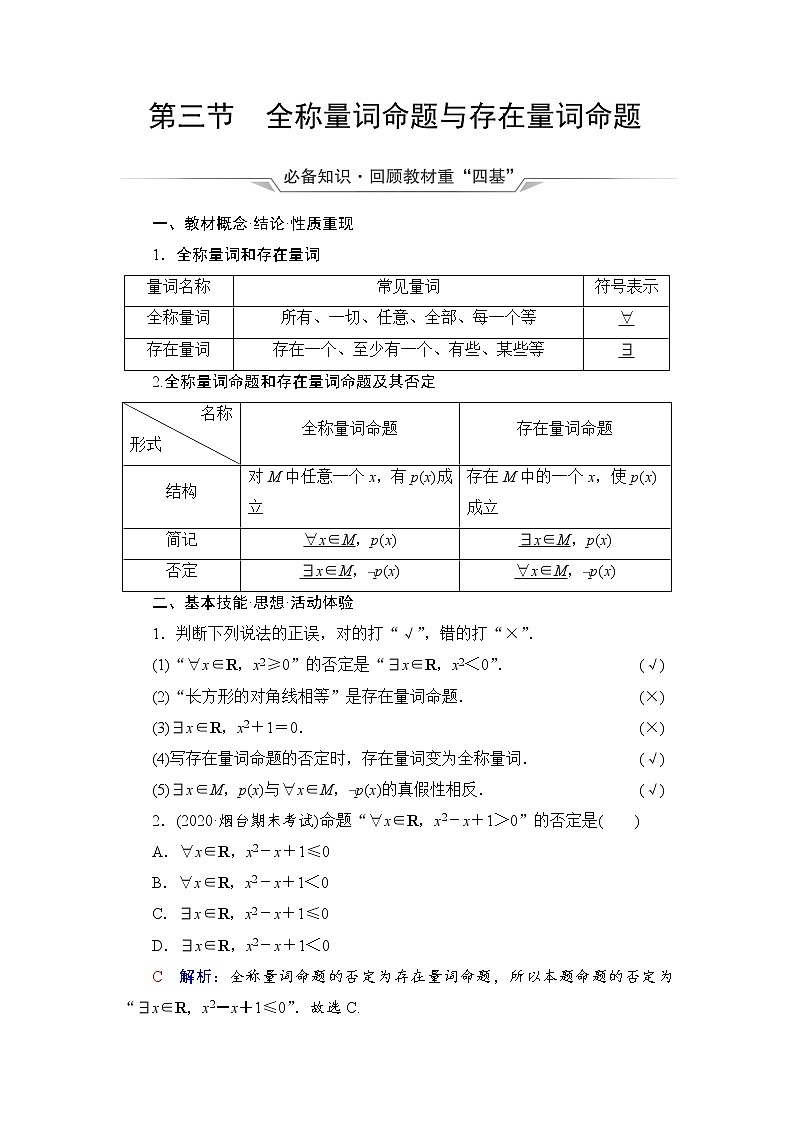
1．全称量词和存在量词
2.全称量词命题和存在量词命题及其否定
二、基本技能·思想·活动体验
1．判断下列说法的正误，对的打“√”，错的打“×”．
(1)“∀x∈R，x2≥0”的否定是“∃x∈R，x2＜0”．(√)
(2)“长方形的对角线相等”是存在量词命题．(×)
(3)∃x∈R，x2＋1＝0．(×)
(4)写存在量词命题的否定时，存在量词变为全称量词．(√)
(5)∃x∈M，p(x)与∀x∈M，p(x)的真假性相反．(√)
2．(2020·烟台期末考试)命题“∀x∈R，x2－x＋1＞0”的否定是( )
A．∀x∈R，x2－x＋1≤0
B．∀x∈R，x2－x＋1＜0
C．∃x∈R，x2－x＋1≤0
D．∃x∈R，x2－x＋1＜0
C 解析：全称量词命题的否定为存在量词命题，所以本题命题的否定为“∃x∈R，x2－x＋1≤0”．故选C.
3．若命题“∀x∈R，x2＋mx＋2≥0”为真命题，则m的取值范围是( )
A．(2eq \r(2)，＋∞)
B．(－2eq \r(2)，2eq \r(2))
C．[－2eq \r(2)，2eq \r(2)]
D．(－∞，－2eq \r(2)]∪[2eq \r(2)，＋∞)
C 解析：∀x∈R，x2＋mx＋2≥0为真命题，等价于f (x)＝x2＋mx＋2的图象与x轴有一个交点或没有交点，故Δ＝m2－8≤0，解得－2eq \r(2)≤m≤2eq \r(2).
考点1 全称量词命题、存在量词命题的否定——基础性
1．(2021·淄博市部分学校高三检测)命题“∃x∈(0，＋∞)，ln x＝x－1”的否定是( )
A．∃x∈(0，＋∞)，ln x≠x－1
B．∃x(0，＋∞)，ln x＝x－1
C．∀x∈(0，＋∞)，ln x≠x－1
D．∀x(0，＋∞)，ln x＝x－1
C 解析：存在量词命题的否定是全称量词命题，将结论加以否定，所以命题的否定为“∀x∈(0，＋∞)，ln x≠x－1”．
2．命题“∀x＞0，eq \f(x,x－1)＞0”的否定是( )
A．∃x＜0，eq \f(x,x－1)≤0
B．∃x＞0，0≤x≤1
C．∀x＞0，eq \f(x,x－1)≤0
D．∀x＜0，0≤x≤1
B 解析：因为eq \f(x,x－1)＞0，所以x＜0或x＞1，所以eq \f(x,x－1)＞0的否定是0≤x≤1，所以命题的否定是∃x＞0，0≤x≤1.故选B．
3．命题“∀x∈R，∃n∈N*，使得n≥x2”的否定形式是( )
A．∀x∈R，∃n∈N*，使得n＜x2
B．∀x∈R，∀n∈N*，使得n＜x2
C．∃x∈R，∃n∈N*，使得n＜x2
D．∃x∈R，∀n∈N*，使得n＜x2
D 解析：“∀x∈R，∃n∈N*，使得n≥x2”的否定形式为“∃x∈R，∀n∈N*，使得n＜x2”．
全称量词命题与存在量词命题的否定
(1)改写量词：确定命题所含量词的类型，省去量词的要结合命题的含义加上量词，再对量词进行改写．
(2)否定结论：对原命题的结论进行否定．
考点2 全称量词命题、存在量词命题的真假判断 ——基础性
1．下列四个命题中的真命题是( )
A．∀n∈R，n2≥n
B．∃n∈R，∀m∈R，m·n＝m
C．∀n∈R，∃m∈R，m20且Δ＝16－4a4.故当原命题为假命题时，a≤4.故选C.
(2)已知f (x)＝x2，g(x)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up8(x)－m.若对∀x1∈[0,3]，∃x2∈[1,2]，使得f (x1)≥g(x2)，则实数m的取值范围是________．
eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(1,4)，＋∞)) 解析：当x∈[0,3]时，f (x)min＝f (0)＝0；当x∈[1,2]时，g(x)min＝g(2)＝eq \f(1,4)－m．
由f (x)min≥g(x)min，得0≥eq \f(1,4)－m，所以m≥eq \f(1,4).
本例(2)中，若将“∃x2∈[1,2]”改为“∀x2∈[1,2]”，其他条件不变，则实数m的取值范围是________．
eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞)) 解析：当x∈[1,2]时，g(x)max＝g(1)＝eq \f(1,2)－m.由f (x)min≥g(x)max，得0≥eq \f(1,2)－m，所以m≥eq \f(1,2).
根据全称(存在)量词命题的真假求参数的思路
此类问题的本质是恒成立问题或有解问题．一般先利用等价转化思想将条件合理转化，得到关于参数的方程或不等式(组)，再通过解方程或不等式(组)求出参数的值或范围．
1．已知函数f (x)＝2ax－a＋3.若∃x0∈(－1,1)，使得f (x0)＝0，则实数a的取值范围是( )
A．(－∞，－3)∪(1，＋∞)B．(－∞，－3)
C．(－3,1)D．(1，＋∞)
A 解析：依题意可得f (－1)·f (1)＜0，即(－2a－a＋3)·(2a－a＋3)＜0，解得a＜－3或a＞1.故选A．
2．已知函数f (x)＝x2－2x＋3，g(x)＝eq \r(x)＋m，对任意的x1，x2∈[1,4]有f (x1)>g(x2)恒成立，则实数m的取值范围是________．
(－∞，0) 解析：f (x)＝x2－2x＋3＝(x－1)2＋2，当x∈[1,4]时，f (x)min＝f (1)＝2，g(x)max＝g(4)＝2＋m，则f (x)min>g(x)max，即2>2＋m，解得m