2020-2021学年天津市河北区九下结课质量检测数学试卷

这是一份2020-2021学年天津市河北区九下结课质量检测数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 下列四个图案中，是中心对称图形的为
A. B.
C. D.

2. 3tan30∘ 的值等于
A. 3B. 2C. 1D. 2

3. 如图所示的机械零件是一个底面为正六边形的直六棱柱，它的主视图是
A. B.
C. D.

4. 二次函数 y=12x+42+5 的图象的开口方向、对称轴、顶点坐标分别是
A. 向上，直线 x=−4，−4,5B. 向下，直线 x=−4，−4,5
C. 向上，直线 x=4，4,−5D. 向上，直线 x=4，4,5

5. 若关于 x 的一元二次方程 mx2+6x−9=0 有两个实数根，则 m 的取值范围是
A. m≤1 且 m≠0B. m≥−1 且 m≠0
C. m≤1D. m≥−1

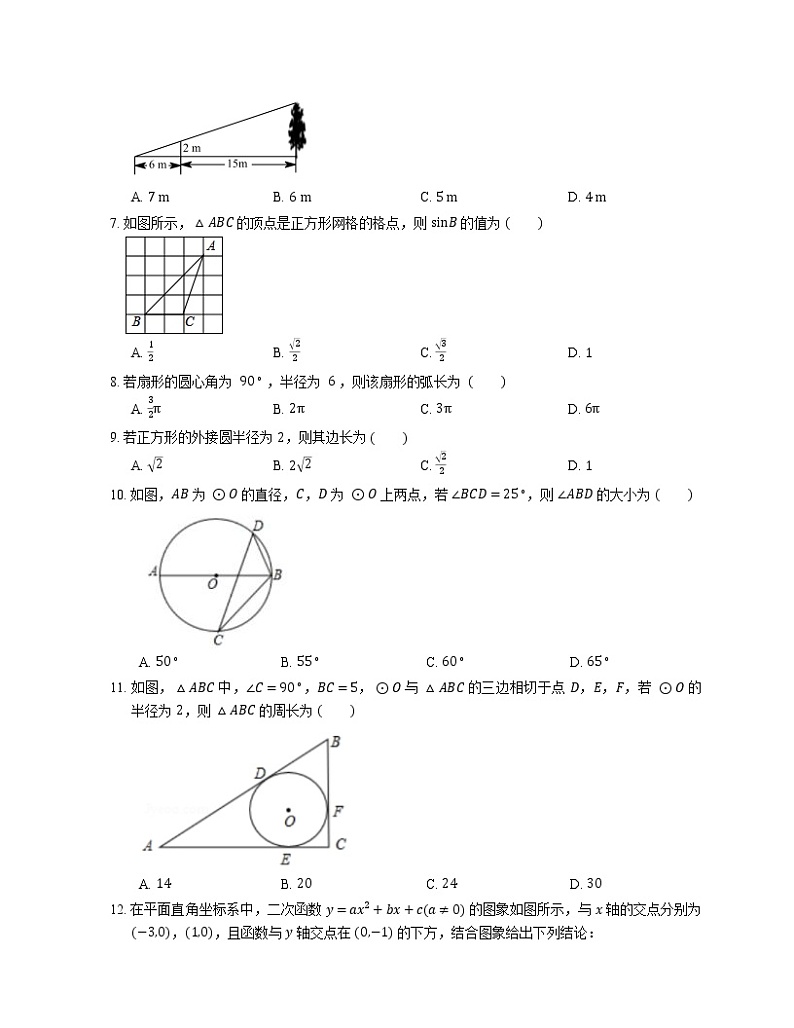
6. 如图，为了测量某棵树的高度，小明用长为 2 m 的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点．此时，竹竿与这一点距离相距 6 m，与树相距 15 m，则树的高度是
A. 7 mB. 6 mC. 5 mD. 4 m

7. 如图所示，△ABC 的顶点是正方形网格的格点，则 sinB 的值为
A. 12B. 22C. 32D. 1

8. 若扇形的圆心角为 90∘ ，半径为 6 ，则该扇形的弧长为
A. 32πB. 2πC. 3πD. 6π

9. 若正方形的外接圆半径为 2，则其边长为
A. 2B. 22C. 22D. 1

10. 如图，AB 为 ⊙O 的直径，C，D 为 ⊙O 上两点，若 ∠BCD=25∘，则 ∠ABD 的大小为
A. 50∘B. 55∘C. 60∘D. 65∘

11. 如图，△ABC 中，∠C=90∘，BC=5，⊙O 与 △ABC 的三边相切于点 D，E，F，若 ⊙O 的半径为 2，则 △ABC 的周长为
A. 14B. 20C. 24D. 30

12. 在平面直角坐标系中，二次函数 y=ax2+bx+ca≠0 的图象如图所示，与 x 轴的交点分别为 −3,0，1,0，且函数与 y 轴交点在 0,−1 的下方，结合图象给出下列结论：
① abc<0；
② b2−4ac<4a；
③当 −2≤x≤3 时，y 的取值范围是 −32b≤y≤6b；
④ 5a−b+2c<−1．
其中，正确的结论是
A. ①②B. ①③C. ①④D. ③④

二、填空题（共6小题；共30分）
13. 在平面直角坐标系中，已知点 A4,−3 与点 B 关于原点对称，则点 B 的坐标是 ．

14. 小明掷一枚质地均匀的硬币 8 次，正面向上的概率为 ．

15. 若 △ABC∽△AʹBʹCʹ，且 △ABC 与 △AʹBʹCʹ 的面积之比为 1:4，则相似比为 ．

16. 在反比例函数 y=1−kx 的图象的每一支上，y 都随 x 的增大而减小，则 k 的取值范围是 ．

17. 若抛物线 y=x2+2x+c 的顶点在 x 轴上，则 c= ．

18. 如图，四边形 ABCD 是边长为 2 的正方形，E 是 BC 边的中点，F 是直线 DE 上的动点．连接 CF，将线段 CF 绕点 C 逆时针旋转 90∘ 得到 CG，连接 EG，则 EG 的最小值是 ．

三、解答题（共6小题；共78分）
19. 解方程：x2+2x−2=0．

20. 如图，小明在自家楼房的窗户 A 处，测量楼前的一棵树 CD 的高．现测得树顶 C 处的俯角为 37∘，树底 D 处的俯角为 45∘，测试点 A 的高度 AB 为 20 米．请你帮助小明计算树的高度（精确到 0.1 米）．
参考数据：sin37∘≈0.602，cs37∘≈0.799，tan37∘≈0.754．

21. 如图，AB 是半圆 O 的直径，C，D 是半圆 O 上的两点，且 OD∥BC，OD 与 AC 交于点 E．
（1）若 ∠B=70∘，求 ∠CAD 的度数；
（2）若 AB=4，AC=3，求 DE 的长．

22. 某种商品的进价为 40 元/件，以获利不低于 20% 的价格销售时，商品的销售单价 y（元/件）与销售数量 x（件）（x 是正整数）之间的关系如下表：
x件⋯5101520⋯y元/件⋯75706560⋯
（1）当销售单价不低于最低销售单价时，y 是 x 的一次函数．求出 y 与 x 的函数关系式及 x 的取值范围；
（2）在 Ⅰ 的条件下，当销售单价为多少元时，所获销售利润最大，最大利润是多少元?

23. 在平面直角坐标系中，O 为原点，点 A3,0，点 B0,4，把 △ABO 绕点 B 逆时针旋转，得 DAʹBOʹ，点 A，O 旋转后的对应点为 Aʹ，Oʹ，记旋转角为 a．
（1）如图①，若 a=90∘，求 AAʹ 的长；
（2）如图②，若 a=45∘，求点 Oʹ 的坐标；
（3）若 M 为 AB 边上的一动点，在 OB 上取一点 N0,1，将 △ABO 绕点 B 逆时针旋转一周，求 MN 的取值范围（直接写出结果即可）．

24. 已知抛物线 y=ax2+bx+c 的顶点为 3,2，且过点 0,11．
（1）求抛物线的解析式；
（2）将抛物线先向左平移 2 个单位长度，再向下平移 mm>0 个单位长度后得到新抛物线．
①若新抛物线与 x 轴交于 A，B 两点（点 A 在点 B 的左侧），且 OB=3OA，求 m 的值；
②若 Px1,y1，Qx2,y2 是新抛物线上的两点，当 n≤x1≤n+1，x2≥4 时，均有 y1≤y2，求 n 的取值范围．
答案
第一部分
1. D
2. A
3. C
4. A
5. B
6. A【解析】如图，
AD=6，AB=21，DE=2，
由于 DE∥BC，
∴△ADE∽△ABC，
得：DEBC=ADAB，即 2BC=621，
解得：BC=7，
故树的高度为 7 m．
7. B
8. C
9. B
10. D
11. D
12. C
第二部分
13. −4,3
14. 12
15. 1:2
16. k<1
17. 1
18. 55
第三部分
19.
∵x2+2x−2=0,∴x2+2x=2,∴x2+2x+1=3,∴x+12=3,∴x=−1?3,∴x1=−1−3,x2=−1+3.
20. 如图，过点 C 作 CE 垂直点 A 所在的水平线于点 E，
则 CE⊥AE，
则四边形 ABDE 为矩形，
∴AE=BD，DE=AB，
由题意可知，AB=20，∠EAC=37∘，∠EAD=45∘，
在 Rt△ADE 中，
∵∠AED=90∘，∠EAD=45∘，
∴∠ADE=∠EAD=45∘，
∴AE=DE=AB=20，
在 Rt△ACE 中，tan∠EAC=CEAE，
∴CE=AE⋅tan37∘≈20×0.754=15.08，
∴CD=ED−CE=20−15.08≈4.9．
答：树的高度约为 4.9 米．
21. （1） ∵AB 是半圆 O 的直径，
∴∠ACB=90∘．
又 ∵OD∥BC，
∴∠AEO=90∘，即 OE⊥AC，
∴∠CAB=90∘−∠B=90∘−70∘=20∘，∠AOD=∠B=70∘．
∵OA=OD，
∴∠DAO=∠ADO=180∘−∠AOD2=180∘−70∘2=55∘，
∴∠CAD=∠DAO−∠CAB=55∘−20∘=35∘．
（2） 在直角 △ABC 中，BC=AB2−AC2=42−32=7．
∵OE⊥AC，
∴AE=EC，
又 ∵OA=OB，
∴OE=12BC=72．
又 ∵OD=12AB=2，
∴DE=OD−OE=2−72．
22. （1） 设一次函数解析式为 y=kx+bk≠0，
根据题意得：75=5k+b,70=10k+b,
解得：k=−1，b=80，
∴y=−x+80，
最低销售单价是 401+20%=48（元），
根据题意得：x>0,−x+80≥48 且 x 为正整数，
∴0 ∴y=−x+80（0 （2） 设所获利润为 P 元，根据题意得：
P=y−40x=−x+80−40x=−x−202+400，
即 P 是 x 的二次函数，
∵a=−1<0，
∴P 有最大值，
∴ 当 x=20 时，P最大值=400，此时 y=60，
∴ 当销售单价为 60 元时，所获利润最大，最大利润为 400 元．
23. （1） 如图①，
∵ 点 A3,0，点 B0,4，
∴OA=3，OB=4，
在 Rt△ABO 中，由勾股定理得
∴AB=32+42=5，
∵△ABO 绕点 B 逆时针旋转 90∘，得 △AʹBOʹ，由旋转的性质，可得
BA=BAʹ=5，∠ABAʹ=90∘，
∴△ABAʹ 为等腰直角三角形，
∴AAʹ=2BA=52．
（2） 过点 Oʹ 作 OʹC⊥y 轴，垂足为 C，如图②，
∵△ABO 绕点 B 逆时针旋转 45∘，得 △AʹBOʹ，
∴BO=BOʹ=4，∠OBOʹ=45∘，
∴ 在 Rt△OʹCB 中，
OʹC=BC=OʹB⋅sin∠OʹBC=OʹB⋅sin45∘=22,
∴OC=BO−BC=4−22，
∴Oʹ 点的坐标为 22,4−22．
（3） 0≤MN≤8．
24. （1） 设二次函数解析式为 y=ax−h2+ka≠0．
∵ 顶点为 3,2，
∴y=ax−32+2a≠0，
又 ∵ 抛物线过点 0,11，
∴a0−32+2=11，
∴a=1．
∴y=x−32+2，
∴ 抛物线的解析式为：y=x2−6x+11；
（2） 抛物线 y=x−32+2 先向左平移 2 个单位长度，再向下平移 m 个单位长度后得新抛物线 y=x−12+2−m=x2−2x+3−m．
①分情况讨论：
若点 A，B 均在 x 轴正半轴上，设 Ax,0，则 B3x,0，
由对称性可知：x+3x2=1，
∴x=12，A12,0．
∴122−2×12+3−m=0．
∴m=94，
若点 A 在 x 轴负半轴上，点 B 在 x 轴正半轴上，设 Ax,0，则 B−3x,0，
由对称性可知：x−3x2=1，
∴x=−1，A−1,0．
∴−12−2×−1+3−m=0．
∴m=6．
综上：m=94 或 m=6；
② ∵ 新抛物线开口向上，对称轴为直线 x=1，
∴ 当 x=4 和 x=−2 时，函数值相等．
又 ∵ 当 n≤x1≤n+1，x2≥4 时，均有 y1≤y2，
∴ 结合图象，得 n≥−2,n+1≤4.
∴−2≤n≤3．