2022届高三新高考开学数学摸底考试卷5含答案

这是一份2022届高三新高考开学数学摸底考试卷5含答案，共19页。试卷主要包含了单项选择题， 多项选择题，填空题，解答题等内容，欢迎下载使用。

2022届新高考开学数学摸底考试卷5

一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）
1．记全集U＝R，集合A＝，集合B＝，则＝
A．[4，) B．(1，4] C．[1，4) D．(1，4)
2．已知，，，则a，b，c的大小关系为
A．b＜a＜c B．a＜b＜c C．c＜b＜a D．c＜a＜b
3．若，，，(0，)，则＝
A． B． C． D．
4．我国即将进入双航母时代，航母编队的要求是每艘航母配2~3艘驱逐舰，1~2艘核潜艇.船厂现有5艘驱逐舰和3艘核潜艇全部用来组建航母编队，则不同的组建方法种数为
A．30 B．60 C．90 D．120
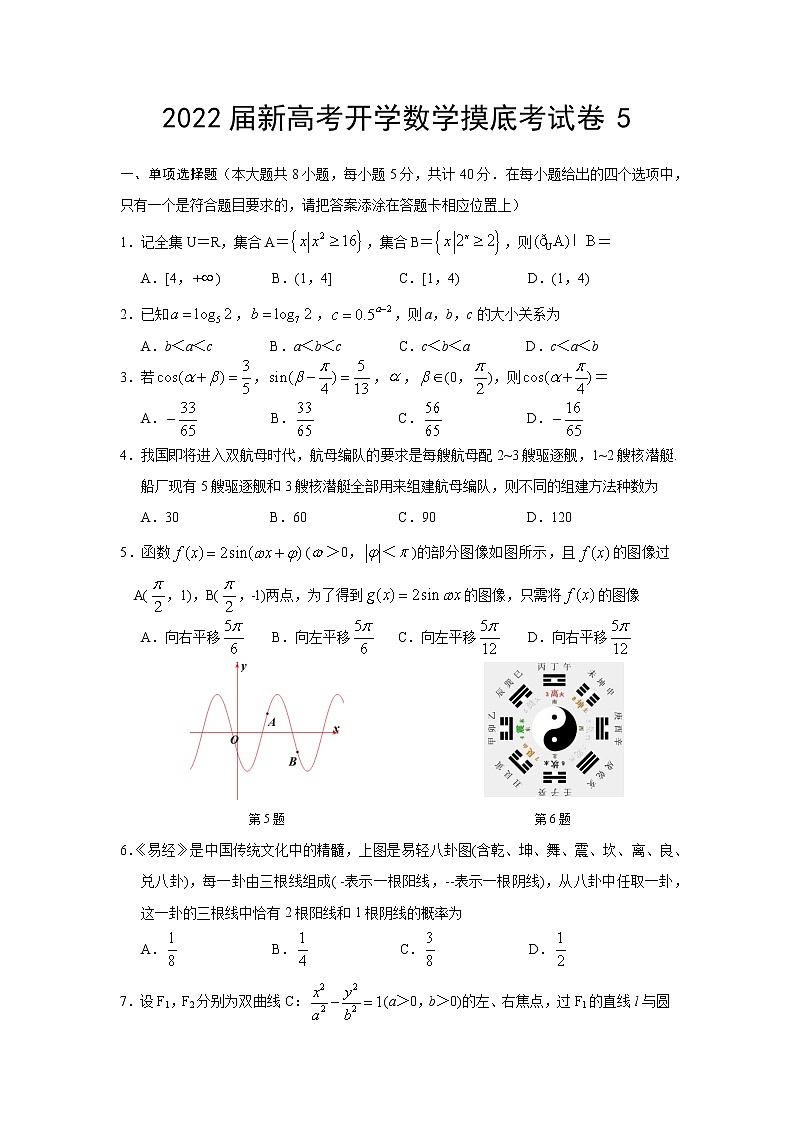
5．函数(＞0，＜)的部分图像如图所示，且的图像过A(，1)，B(，﹣1)两点，为了得到的图像，只需将的图像
A．向右平移 B．向左平移 C．向左平移 D．向右平移

第5题 第6题
6．《易经》是中国传统文化中的精髓，上图是易轻八卦图(含乾、坤、舞、震、坎、离、良、兑八卦)，每一卦由三根线组成( -表示一根阳线，--表示一根阴线)，从八卦中任取一卦，这一卦的三根线中恰有2根阳线和1根阴线的概率为
A． B． C． D．
7．设F1，F2分别为双曲线C：(a＞0，b＞0)的左、右焦点，过F1的直线l与圆O：相切，l与C的渐近线在第一象限内的交点是P，若PF2⊥x轴，则双曲线的离心率等于
A． B．2 C． D．4
8．对于函数，若存在区间[a，b]，当x[a，b]时的值域为[ka，kb](k＞0)，则称为k倍值函数．若是k倍值函数，则实数k的取值范围是
A．(e＋1，) B．(e＋2，) C．(，) D．(，)
二、 多项选择题（本大题共4小题，每小题5分， 共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）
9．下列说法正确的是
A．将一组数据中的每个数据都乘以同一个非零常数a后，方差也变为原来的a倍
B．设有一个回归方程y＝3﹣5x，变量x增加1个单位时，y平均减少5个单位
C．线性相关系数r越大，两个变量的线性相关性越强；反之，线性相关性越弱
D．在某项测量中，测量结果服从正态分布N(1，)(＞0)，则P(＞1)＝0.5
10．已知抛物线C：过点P(1，1)，则下列结论正确的是
A．点P到抛物线焦点的距离为
B．过点P作过抛物线焦点的直线交抛物线于点Q，则△OPQ的面积为
C．过点P与抛物线相切的直线方程为x﹣2y＋1＝0
D．过P作两条斜率互为相反数的直线交抛物线于点M，N，则直线MN的斜率为定值
11．在△ABC中，已知bcosC＋ccosB＝2b，且，则
A．a，b，c成等比数列 B．sinA：sinB：sinC＝2：1：
C．若a＝4，则S△ABC＝ D．A，B，C成等差数列
12．已知函数，若，则下列选项正确的是
A．
B．
C．
D．当时，
三、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）
13．高二某班共有60名学生，其中女生有20名，三好学生占全班人数的，而且三好学生中女生占一半．现在从该班任选一名同学参加某一座谈会．则在已知没有选上女生的条件下，选上的是三好学生的概率为 ．
14．曲线的一条切线的斜率为2，则该切线的方程为 ．
15．已知P是边长为2的正六边形ABCDEF内的一点，则的取值范围是 ．
16．椭圆与双曲线有相同的焦点F1(﹣c，0)，F2(c，0)，椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行．若椭圆与双曲线的离心率分别为，，则＝ ；且的最小值为 ．
四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）
17．（本小题满分10分）
已知函数．
（1）求函数的单调递增区间；
（2）在△ABC中，内角A，B，C所对的边分别为a，b，c，若，C＝，c＝2，求△ABC的面积．












18．（本小题满分12分）
2020年寒假是特殊的寒假，因为疫情全体学生只能在家进行网上在线学习，为了研究学生在网上学习的情况，某学校在网上随机抽取120名学生对线上教育进行调查，其中男生与女生的人数之比为11：13，其中男生30人对于线上教育满意，女生中有15名表示对线上教育不满意．

满意
不满意
总计
男生



女生



合计


120
（1）完成2×2列联表，并回答能否有99%的把握认为对“线上教育是否满意与性别有关”；
（2）从被调查中对线上教育满意的学生中，利用分层抽样抽取8名学生，再在8名学生中抽取3名学生，作学习经验介绍，其中抽取男生的个数为．求出的分布列及期望值．
附公式及表：
，其中．

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828








19．（本小题满分12分）
已知椭圆C的中心在原点，其焦点与双曲线的焦点重合，点P(0，)在椭圆C上，动直线l：y＝kx＋m交椭圆于不同两点A，B，且(O为坐标原点)．
（1）求椭圆的方程；
（2）讨论7m2﹣12k2是否为定值；若是，求出该定值；若不是，请说明理由．








20．（本小题满分12分）
已知函数，且的解集为[﹣1，2]．
（1）求函数的解析式；
（2）解关于x的不等式(m≥0)；
（3）设，若对于任意的，[﹣2，1]都有，求M的最小值．



21．（本小题满分12分）
已知．
（1）讨论的单调性；
（2）当a＝1时，证明对于任意的[1，2]成立．



22．（本小题满分12分）
已知点P是抛物线C1：的准线上任意一点，过点P作抛物线的两条切线PA、PB，其中A、B为切点．
（1）证明：直线AB过定点，并求出定点的坐标；
（2）若直线AB交椭圆C2：于C、D两点，S1，S2分别是△PAB，△PCD的面积，求的最小值．

2022届新高考开学数学摸底考试卷5
（教师版）

一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）
1．记全集U＝R，集合A＝，集合B＝，则＝
A．[4，) B．(1，4] C．[1，4) D．(1，4)
答案：C
解析：∵集合A＝，
∴，又∵B＝，
∴＝[1，4)，故选C．
2．已知，，，则a，b，c的大小关系为
A．b＜a＜c B．a＜b＜c C．c＜b＜a D．c＜a＜b
答案：A
解析：∵，∴，∴，∴，
又，，∴b＜a＜c，故选A．
3．若，，，(0，)，则＝
A． B． C． D．
答案：C
解析：∵，(0，)，∴(0，π)，(，)，
∴，，
∴
，故选C．
4．我国即将进入双航母时代，航母编队的要求是每艘航母配2~3艘驱逐舰，1~2艘核潜艇.船厂现有5艘驱逐舰和3艘核潜艇全部用来组建航母编队，则不同的组建方法种数为
A．30 B．60 C．90 D．120
答案：B
解析：有两种情况，①一艘航母配2搜驱逐舰和1搜核潜艇，另一艘航母配3搜驱逐舰和2搜核潜艇，②一艘航母配2搜驱逐舰和2搜核潜艇，另一艘航母配3搜驱逐舰和1搜核潜艇，，故选B．
5．函数(＞0，＜)的部分图像如图所示，且的图像过A(，1)，B(，﹣1)两点，为了得到的图像，只需将的图像

A．向右平移 B．向左平移 C．向左平移 D．向右平移
答案：C
解析：由题意知，，∴＝2，，，
∵＜，∴，∴，故选C．
6．《易经》是中国传统文化中的精髓，上图是易轻八卦图(含乾、坤、舞、震、坎、离、良、兑八卦)，每一卦由三根线组成( -表示一根阳线，--表示一根阴线)，从八卦中任取一卦，这一卦的三根线中恰有2根阳线和1根阴线的概率为

A． B． C． D．
答案：C
解析：P＝，故选C．
7．设F1，F2分别为双曲线C：(a＞0，b＞0)的左、右焦点，过F1的直线l与圆O：相切，l与C的渐近线在第一象限内的交点是P，若PF2⊥x轴，则双曲线的离心率等于
A． B．2 C． D．4
答案：A
解析：，，，，故选A．
8．对于函数，若存在区间[a，b]，当x[a，b]时的值域为[ka，kb](k＞0)，则称为k倍值函数．若是k倍值函数，则实数k的取值范围是
A．(e＋1，) B．(e＋2，) C．(，) D．(，)
答案：B
解析：是单调增函数，故，故a，b是方程的两个根，令，，当k＞2，x＝时，有最小值为，解得k＞e＋2，故选B．
二、 多项选择题（本大题共4小题，每小题5分， 共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）
9．下列说法正确的是
A．将一组数据中的每个数据都乘以同一个非零常数a后，方差也变为原来的a倍
B．设有一个回归方程y＝3﹣5x，变量x增加1个单位时，y平均减少5个单位
C．线性相关系数r越大，两个变量的线性相关性越强；反之，线性相关性越弱
D．在某项测量中，测量结果服从正态分布N(1，)(＞0)，则P(＞1)＝0.5
答案：BD
解析：选项A，方差变为原来的a2倍，故A错误；线性相关系数r的绝对值越大，两个变量的线性相关性越强；线性相关系数r的绝对值越接近0，线性相关性越弱，由此可见C错误，故选BD．
10．已知抛物线C：过点P(1，1)，则下列结论正确的是
A．点P到抛物线焦点的距离为
B．过点P作过抛物线焦点的直线交抛物线于点Q，则△OPQ的面积为
C．过点P与抛物线相切的直线方程为x﹣2y＋1＝0
D．过P作两条斜率互为相反数的直线交抛物线于点M，N，则直线MN的斜率为定值
答案：BCD
解析：∵抛物线C：过点P(1，1)，∴，∴，故该抛物线焦点坐标为(，0)，准线方程为x＝，故点P到抛物线焦点的距离为，故A错误；△OPQ的面积，故B正确；设过点P的直线方程为，与抛物线联立并化简得，，解得k＝，故过点P与抛物线相切的直线方程为x﹣2y＋1＝0，C正确；设PM的斜率为k，则PN的斜率为﹣k，求得M(，)，N(，)，求得MN的斜率为，D正确，故选BCD．
11．在△ABC中，已知bcosC＋ccosB＝2b，且，则
A．a，b，c成等比数列 B．sinA：sinB：sinC＝2：1：
C．若a＝4，则S△ABC＝ D．A，B，C成等差数列
答案：BC
解析：由得，，，故ab＝c2，故a，c，b成等比数列，故A错误；∵bcosC＋ccosB＝2b，∴a＝2b，又ab＝c2，∴c＝b，∴a：b：c＝2：1：，∴sinA：sinB：sinC＝2：1：，故B正确；cosC＝，sinC＝，∴S＝，故C正确；cosB＝，故B≠60°，故D错误，故选BC．
12．已知函数，若，则下列选项正确的是
A．
B．
C．
D．当时，
答案：CD
解析：首先注意到函数，在(0，)单调递减，在(，)单调递增，故A错误，，故D正确；令，不是单调函数，故B错误；令，是单调增函数，故C正确，故选CD．
三、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）
13．高二某班共有60名学生，其中女生有20名，三好学生占全班人数的，而且三好学生中女生占一半．现在从该班任选一名同学参加某一座谈会．则在已知没有选上女生的条件下，选上的是三好学生的概率为 ．
答案：
解析：P＝．
14．曲线的一条切线的斜率为2，则该切线的方程为 ．
答案：
解析：，，设切点横坐标为，，所以切点(1，2)，故切线方程为，即．
15．已知P是边长为2的正六边形ABCDEF内的一点，则的取值范围是 ．
答案：(﹣2，6)
解析：点P与点F重合时，有最小值为﹣2，当点P与点C重合时，有最大值为6，故的取值范围是(﹣2，6)．
16．椭圆与双曲线有相同的焦点F1(﹣c，0)，F2(c，0)，椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行．若椭圆与双曲线的离心率分别为，，则＝ ；且的最小值为 ．
答案：1；
解析：设椭圆方程为，双曲线方程为，则由直线F1B与双曲线的一条渐近线平行，得，∴＝1；
所以，当且仅当取等号．
四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）
17．（本小题满分10分）
已知函数．
（1）求函数的单调递增区间；
（2）在△ABC中，内角A，B，C所对的边分别为a，b，c，若，C＝，c＝2，求△ABC的面积．
解：（1）∵sin2x﹣cos2x
＝2sin（2x），
令2kπ2x2kπ，k∈Z，解得kπx≤kπ，k∈Z，
∴函数f（x）的单调递增区间为：[kπ，kπ]，k∈Z．
（2）∵f（A）＝2sin（2A）＝2，
∴sin（2A）＝1，
∵A∈（0，π），2A∈（，），
∴2A，解得A，
∵C，c＝2，
∴由正弦定理，可得，
∴S△ABCabsinC（1）．
18．（本小题满分12分）
2020年寒假是特殊的寒假，因为疫情全体学生只能在家进行网上在线学习，为了研究学生在网上学习的情况，某学校在网上随机抽取120名学生对线上教育进行调查，其中男生与女生的人数之比为11：13，其中男生30人对于线上教育满意，女生中有15名表示对线上教育不满意．

满意
不满意
总计
男生



女生



合计


120
（1）完成2×2列联表，并回答能否有99%的把握认为对“线上教育是否满意与性别有关”；
（2）从被调查中对线上教育满意的学生中，利用分层抽样抽取8名学生，再在8名学生中抽取3名学生，作学习经验介绍，其中抽取男生的个数为．求出的分布列及期望值．
附公式及表：
，其中．

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
解：（1）因为男生人数为：，所以女生人数为，
于是可完成列联表，如下：

满意
不满意
总计
男生
30
25
55
女生
50
15
65
合计
80
40
120
根据列联表中的数据，得到的观测值
，
所以有99%的把握认为对“线上教育是否满意与性别有关”
（2）由（1）可知男生抽3人，女生抽5人，依题可知的可能取值为，并且服从超几何分布，，即
,
.
可得分布列为

0
1
2
3





可得.
19．（本小题满分12分）
已知椭圆C的中心在原点，其焦点与双曲线的焦点重合，点P(0，)在椭圆C上，动直线l：y＝kx＋m交椭圆于不同两点A，B，且(O为坐标原点)．
（1）求椭圆的方程；
（2）讨论7m2﹣12k2是否为定值；若是，求出该定值；若不是，请说明理由．
解：（1）因为双曲线的焦点为，所以在椭圆C中，
设椭圆C的方程为，
由点在椭圆C上得，解得，则，
所以椭圆C的方程为
（2）为定值，理由如下：
设，由可知，
联立方程组，
由得，
，①
由及得，
整理得，
将①式代入上式可得，
同时乘以可化简得，
所以，即为定值.
20．（本小题满分12分）
已知函数，且的解集为[﹣1，2]．
（1）求函数的解析式；
（2）解关于x的不等式(m≥0)；
（3）设，若对于任意的，[﹣2，1]都有，求M的最小值．
解：（1）因为的解集为，所以的根为，2，
所以，，即，；所以；
（2），化简有，整理，
所以当时，不等式的解集为，
当时，不等式的解集为，
当时，不等式的解集为，
当时，不等式的解集为，
（3）因为时，根据二次函数的图像性质，有，
则有，所以，，
因为对于任意的都有，
即求，转化为，
而，，所以，
此时可得，
所以M的最小值为.
21．（本小题满分12分）
已知．
（1）讨论的单调性；
（2）当a＝1时，证明对于任意的[1，2]成立．
解：（1）的定义域为；
.
当，时，，单调递增；
，单调递减.
当时，.
① ，，
当或时，，单调递增；
当时，，单调递减；
② 时，，在内，，单调递增；
③ 时，，
当或时，，单调递增；
当时，，单调递减.
综上所述，
当时，函数在内单调递增，在内单调递减；
当时，在内单调递增，在内单调递减，在内单调递增；
当时，在内单调递增；
当，在内单调递增，在内单调递减，在内单调递增.
（2）由（Ⅰ）知，时，
，，
令，.
则，
由可得，当且仅当时取得等号.
又，
设，则在单调递减，
因为，
所以在上存在使得时，时，，
所以函数在上单调递增；在上单调递减，
由于，因此，当且仅当取得等号，
所以，
即对于任意的恒成立
22．（本小题满分12分）
已知点P是抛物线C1：的准线上任意一点，过点P作抛物线的两条切线PA、PB，其中A、B为切点．
（1）证明：直线AB过定点，并求出定点的坐标；
（2）若直线AB交椭圆C2：于C、D两点，S1，S2分别是△PAB，△PCD的面积，求的最小值．

解：（1）证明：设点、，
则以为切点的切线方程为，即，
同理以为切点的切线方程为，
两条切线均过点，，即，
所以，点、的坐标满足直线的方程，
所以，直线的方程为，
在直线的方程中，令，可得，所以，直线过定点；
（2）设点到直线的距离为，则.
由题意可知，直线不与轴重合，可设直线的方程为，
设、，由，得，恒成立，
由韦达定理得，，
由弦长公式可得
由，得，恒成立.
由韦达定理得，，
由弦长公式得.
，
当且仅当时，等号成立.
因此，的最小值为.