

2021全国中考数学真题分类汇编--三角形 特殊三角形
展开2021全国中考真题分类汇编(三角形)
----特殊三角形
一、选择题
1. (2021•江苏省扬州)如图,在的正方形网格中有两个格点A、B,连接,在网格中再找一个格点C,使得是等腰直角三角形,满足条件的格点C的个数是( )
A. 2 B. 3 C. 4 D. 5
2. (2021•山东省临沂市)如图,点A,B都在格点上,若BC=,则AC的长为( )
A. B. C.2 D.3
3. (2021•山西)在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理.这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的 许多数学公式和规律,它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
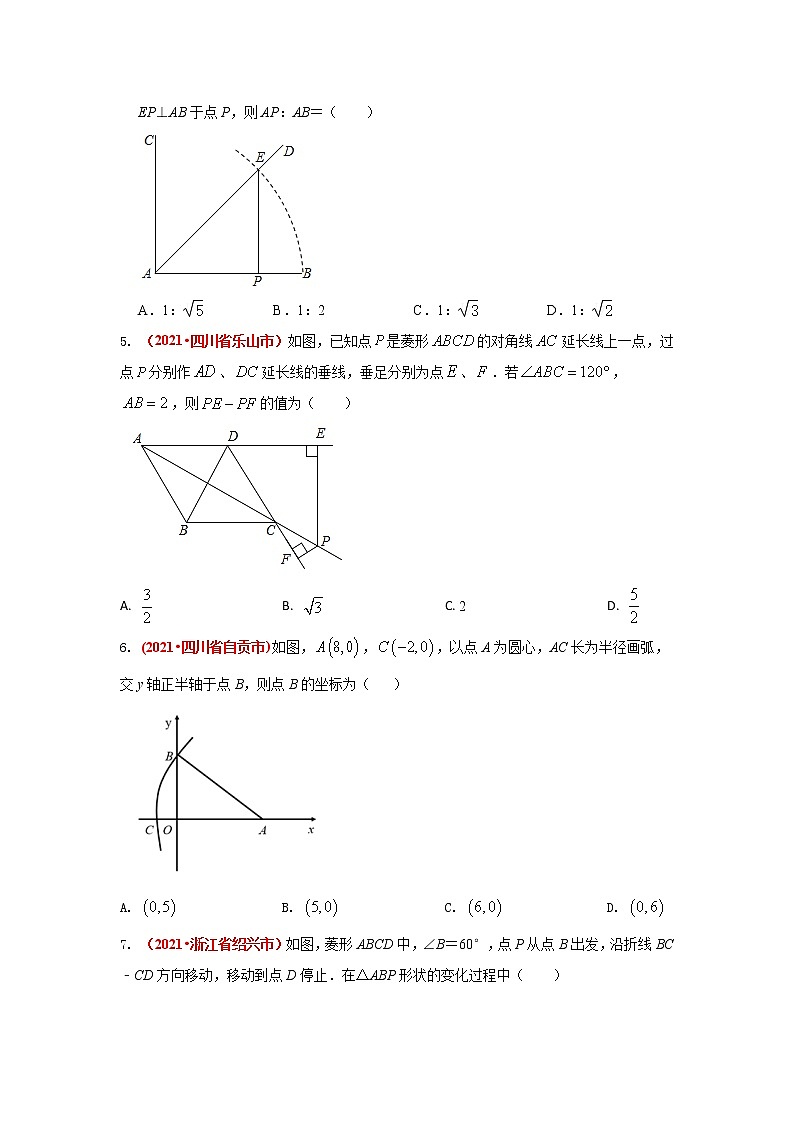
4. (2021•浙江省杭州)已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD,③以点A为圆心,AB长为半径作弧,交AD于E;④过点E作EP⊥AB于点P,则AP:AB=( )
A.1: B.1:2 C.1: D.1:
5. (2021•四川省乐山市)如图,已知点是菱形的对角线延长线上一点,过点分别作、延长线的垂线,垂足分别为点、.若,,则的值为( )
A. B. C. 2 D.
6. (2021•四川省自贡市)如图,,,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
A. B. C. D.
7. (2021•浙江省绍兴市)如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC﹣CD方向移动,移动到点D停止.在△ABP形状的变化过程中( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
8. (2021•新疆)如图,在Rt中,,,,于点D,E是AB的中点,则DE的长为( )
A. 1 B. 2 C. 3D. 4
9. (2021•浙江省宁波市)如图,在中,于点D,.若E,F分别为,中点,则的长为( )
A. B. C. 1 D.
10. (2021•甘肃省定西市)如图1,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图象如图2,则AC的长为( )
A.3 B.6 C.8 D.9
11. (2021•广西玉林市)图(1),在中,,点从点出发,沿三角形边以/秒的速度逆时针运动一周,图(2)是点运动时,线段的长度()随运动时间(秒)变化的关系图象,则图(2)中点的坐标是( )
A. B.
C. D.
12. (2021•江苏省无锡市)在Rt△ABC中,∠A=90°,AB=6,AC=8,点P是△ABC所在平面内一点,则PA2+PB2+PC2取得最小值时,下列结论正确的是( )
A.点P是△ABC三边垂直平分线的交点
B.点P是△ABC三条内角平分线的交点
C.点P是△ABC三条高的交点
D.点P是△ABC三条中线的交点
13. (2021•贵州省铜仁市)如图,在中,,,,按下列步骤作图:步骤1:以点为圆心,小于的长为半径作弧分别交、于点、.步骤2:分别以点、为圆心,大于的长为半径作弧,两弧交于点.步骤3:作射线交于点.则的长为( )
A. 6 B. C. D.
14. (2021•襄阳市)我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiǎ)生其中,出水一尺,引葭赴岸,适与岸齐.间水深几何.”(丈、尺是长度单位,1丈尺,)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度是多少?则水深为( )
A. 10尺 B. 11尺 C. 12尺 D. 13尺
15.(2021•吉林省长春市)在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法不正确的是( )
A. B. C. D.
16. (2021•湖北省黄石市)如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A. 3 B. C. D.
17. (2021•绥化市)已知在中,,.点为边上的动点,点为边上的动点,则线段的最小值是( )
A. B. C. D.
18. (2021•辽宁省本溪市)如图,在中,,由图中的尺规作图痕迹得到的射线与交于点E,点F为的中点,连接,若,则的周长为( )
A. B. C. D. 4
二.填空题
1. (2021•湖北省黄冈市)在Rt△ABC中,∠C=90°,∠B=30°,适当长为半径画弧,分别交AC,F;再分别以点E,F为圆心EF的长为半径画弧,两弧交于点P,作射线AD交BC于点D,则BD与CD的数量关系为: .
2. (2021•江苏省苏州市)如图,在Rt△ABC中,∠C = 90°.AF = EF.若∠CFE = 72°.则∠B = ▲ °.
3. (2021•江苏省扬州) 如图,在中,,点D是的中点,过点D作,垂足为点E,连接,若,,则________.
4. (2021•湖南省娄底市)如图,中,是上任意一点,于点于点F,若,则________.
5. (2021•四川省成都市)如图,数字代表所在正方形的面积,则A所代表的正方形的面积为 .
6. (2021•四川省眉山市)如图,△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于点M和点N,作直线MN,交AD于点E,则DE的长为 .
7. (2021•浙江省杭州)如图,在直角坐标系中,以点A(3,1),AC,AD(1,1),点C(1,3),点D(4,4)(5,2),则∠BAC ∠DAE(填“>”、“=”、“<”中的一个).
8. (2021•浙江省绍兴市))如图,在△ABC中,AB=AC,∠ABC=70°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连结AP,则∠BAP的度数是 .
9. (2021•江苏省盐城市)如图,在Rt△ABC中,CD为斜边AB上的中线,若CD=2,则AB= .
10. (2021•齐齐哈尔市)若直角三角形其中两条边的长分别为3,4,则该直角三角形斜边上的高的长为________.
11. (2021•贵州省铜仁市)如图,将边长为1的正方形ABCD绕点顺时针旋转到的位置,则阴影部分的面积是______________;
12. (2021•深圳)如图,已知,是角平分线且,作的垂直平分线交于点F,作,则周长为________.
13. (2021•江苏省南京市) 如图,在四边形中,.设,则______(用含的代数式表示).
14. (2021•广西贺州市)如图,一次函数与坐标轴分别交于,两点,点,分别是线段,上的点,且,,则点的标为________.
三、解答题
1. (2021•江西省)如图,在△ABC中,∠A=40°,∠ABC=80°,BE平分∠ABC交AC于点E,ED⊥AB于点D,求证:AD=BD.
2. (2021•浙江省杭州)如图,在△ABC中,∠ABC的平分线BD交AC边于点D,∠C=45°.
(1)求证:AB=BD;
(2)若AE=3,求△ABC的面积.
3. (2021•长沙市)如图,在中,,垂足,,延长至,使得,连接.
(1)求证:;
(2)若,,求的周长和面积.
答案
一、选择题
1. (2021•江苏省扬州)如图,在的正方形网格中有两个格点A、B,连接,在网格中再找一个格点C,使得是等腰直角三角形,满足条件的格点C的个数是( )
A. 2 B. 3 C. 4 D. 5
【答案】B
【解析】
【分析】根据题意,结合图形,分两种情况讨论:①AB为等腰直角△ABC底边;②AB为等腰直角△ABC其中的一条腰.
【详解】解:如图:分情况讨论:
①AB为等腰直角△ABC底边时,符合条件的C点有0个;
②AB为等腰直角△ABC其中的一条腰时,符合条件的C点有3个.
故共有3个点,
故选:B.
2. (2021•山东省临沂市)如图,点A,B都在格点上,若BC=,则AC的长为( )
A. B. C.2 D.3
【分析】根据勾股定理可以得到AB的长,然后由图可知AC=AB﹣BC,然后代入数据计算即可.
【解答】解:由图可得,
AB====2,
∵BC=,
∴AC=AB﹣BC=2﹣=,
故选:B.
3. (2021•山西)在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理.这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的 许多数学公式和规律,它体现的数学思想是(C )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
4. (2021•浙江省杭州)已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD,③以点A为圆心,AB长为半径作弧,交AD于E;④过点E作EP⊥AB于点P,则AP:AB=( )
A.1: B.1:2 C.1: D.1:
【分析】直接利用基本作图方法得出AP=PE,再结合等腰直角三角形的性质表示出AE,AP的长,即可得出答案.
【解答】解:∵AC⊥AB,
∴∠CAB=90°,
∵AD平分∠BAC,
∴∠EAB=×90°=45°,
∵EP⊥AB,
∴∠APE=90°,
∴∠EAP=∠AEP=45°,
∴AP=PE,
∴设AP=PE=x,
故AE=AB=x,
∴AP:AB=x:x=1:.
故选:D.
5. (2021•四川省乐山市)如图,已知点是菱形的对角线延长线上一点,过点分别作、延长线的垂线,垂足分别为点、.若,,则的值为( )
A. B. C. 2 D.
【答案】B
【解析】
【分析】根据菱形的基性质,得到∠PAE=30°,,利用勾股理求出AC=,则AP= +PC,PE=AP=+PC ,由∠PCF=∠DCA=30°,得到PF=PC ,最后算出结果.
【详解】解:∵四边形ABCD是菱形且∠ABC=120°,AB=2,
∴AB=BC=CD=DA=2,∠BAD=60°,AC⊥BD,
∴∠CAE=30︒,
∵AC⊥BD,∠CAE=30°,AD=2,
∴AC=,
∴AP=+PC,
在直角△AEP中,
∵∠PAE=30°,AP=+PC,
∴PE=AP=+PC,
在直角△PFC中,
∵∠PCF=30°,
∴PF=PC,
∴=+PC-PC=,
故选:B.
6. (2021•四川省自贡市)如图,,,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
A. B. C. D.
【答案】D
【解析】
【分析】先根据题意得出OA=8,OC=2,再根据勾股定理计算即可
【详解】解:由题意可知:AC=AB
∵,
∴OA=8,OC=2
∴AC=AB=10
在Rt△OAB中,
∴B(0,6)
故选:D
7. (2021•浙江省绍兴市)如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC﹣CD方向移动,移动到点D停止.在△ABP形状的变化过程中( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
【分析】把点P从点B出发,沿折线BC﹣CD方向移动的整个过程,逐次考虑确定三角形的形状即可。
【解答】解:∵∠B=60°,故菱形由两个等边三角形组合而成,
当AP⊥BC时,此时△ABP为等腰三角形;
当点P到达点C处时,此时△ABP为等边三角形;
当点P在CD上且位于AB的中垂线时,则△ABP为等腰三角形;
当点P与点D重合时,此时△ABP为等腰三角形,
故选:C.
8. (2021•新疆)如图,在Rt中,,,,于点D,E是AB的中点,则DE的长为( )
A. 1 B. 2 C. 3D. 4
【答案】A
9. (2021•浙江省宁波市)如图,在中,于点D,.若E,F分别为,中点,则的长为( )
A. B. C. 1 D.
【答案】C
【解析】
【分析】根据条件可知△ABD为等腰直角三角形,则BD=AD,△ADC是30°、60°的直角三角形,可求出AC长,再根据中位线定理可知EF=。
【详解】解:因为AD垂直BC,
则△ABD和△ACD都是直角三角形,
又因为
所以AD=,
因为sin∠C=,
所以AC=2,
因为EF为△ABC的中位线,
所以EF==1,
故选:C.
10. (2021•甘肃省定西市)如图1,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图象如图2,则AC的长为( )
A.3 B.6 C.8 D.9
【分析】先根据AB=BC结合图2得出AB=,进而利用勾股定理得,AD²+BD²=13,再由运动结合△ADM的面积的变化,得出点M和点B重合时,△ADM的面积最大,其值为3,即AD•BD=3,进而建立二元二次方程组求解,即可得出结论.
【解答】解:由图2知,AB+BC=2,
∵AB=BC,
∴AB=,
∵AB=BC,BD⊥BC,
∴AC=2AD,∠ADB=90°,
在Rt△ABD中,AD²+BD²=AB²=13①,
设点M到AC的距离为h,
∴S△ADM=AD•h,
∵动点M从A点出发,沿折线AB→BC方向运动,
∴当点M运动到点B时,△ADM的面积最大,即h=BD,
由图2知,△ADM的面积最大为3,
∴AD•BC=3,
∴AD•BD=6②,
①+2×②得,AD²+BD²+2AD•BD=13+2×6=25,
∴(AD+BD)²=25,
∴AD+BD=5(负值舍去),
∴BD=5﹣AD③,
将③代入②得,AD(5﹣AD)=6,
∴AD=3或AD=2,
∵AD>BD,
∴AD=3,
∴AC=2AD=6,
故选:B.
11. (2021•广西玉林市)图(1),在中,,点从点出发,沿三角形边以/秒的速度逆时针运动一周,图(2)是点运动时,线段的长度()随运动时间(秒)变化的关系图象,则图(2)中点的坐标是( )
A. B.
C. D.
【答案】C
12. (2021•江苏省无锡市)在Rt△ABC中,∠A=90°,AB=6,AC=8,点P是△ABC所在平面内一点,则PA2+PB2+PC2取得最小值时,下列结论正确的是( )
A.点P是△ABC三边垂直平分线的交点
B.点P是△ABC三条内角平分线的交点
C.点P是△ABC三条高的交点
D.点P是△ABC三条中线的交点
【分析】过P作PD⊥AC于D,过P作PE⊥AB于E,延长CP交AB于M,延长BP交AC于N,设AD=PE=x,AE=DP=y,则AP2+CP2+BP2=3(x﹣2)2+3(y﹣)2+,当x=2,y=时,AP2+CP2+BP2的值最大,此时AD=PE=2,AE=PD=,由=,得AM=4,M是AB的中点,同理可得AN=AC,N为AC中点,即P是△ABC三条中线的交点.
【解答】解:过P作PD⊥AC于D,过P作PE⊥AB于E,延长CP交AB于M,延长BP交AC于N,如图:
∵∠A=90°,PD⊥AC,PE⊥AB,
∴四边形AEPD是矩形,
设AD=PE=x,AE=DP=y,
Rt△AEP中,AP2=x2+y2,
Rt△CDP中,CP2=(6﹣x)2+y2,
Rt△BEP中,BP2=x2+(8﹣y)2,
∴AP2+CP2+BP2=x2+y2+(6﹣x)2+y2+x2+(8﹣y)2
=3x2﹣12x+3y2﹣16y+100
=3(x﹣2)2+3(y﹣)2+,
∴x=2,y=时,AP2+CP2+BP2的值最大,
此时AD=PE=2,AE=PD=,
∵∠A=90°,PD⊥AC,
∴PD∥AB,
∴=,即=,
∴AM=4,
∴AM=AB,即M是AB的中点,
同理可得AN=AC,N为AC中点,
∴P是△ABC三条中线的交点,
故选:D.
13. (2021•贵州省铜仁市)如图,在中,,,,按下列步骤作图:步骤1:以点为圆心,小于的长为半径作弧分别交、于点、.步骤2:分别以点、为圆心,大于的长为半径作弧,两弧交于点.步骤3:作射线交于点.则的长为( )
A. 6 B. C. D.
【答案】B
14. (2021•襄阳市)我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiǎ)生其中,出水一尺,引葭赴岸,适与岸齐.间水深几何.”(丈、尺是长度单位,1丈尺,)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度是多少?则水深为( )
A. 10尺 B. 11尺 C. 12尺 D. 13尺
【答案】C
15. (2021•吉林省长春市)在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法不正确的是( )
A. B. C. D.
【分析】根据等腰三角形的定义一一判断即可.
【解答】解:A、由作图可知AD是△ABC的角平分线,推不出△ADC是等腰三角形,本选项符合题意.
B、由作图可知CA=CD,△ADC是等腰三角形,本选项不符合题意.
C、由作图可知DA=CD,△ADC是等腰三角形,本选项不符合题意.
D、由作图可知BD=CD,推出AD=DC=BD,△ADC是等腰三角形,本选项不符合题意.
故选:A.
16. (2021•湖北省黄石市)如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A. 3 B. C. D.
【答案】A
【解析】
【分析】由尺规作图痕迹可知,BD是∠ABC的角平分线,过D点作DH⊥AB于H点,设DC=DH=x则AD=AC-DC=8-x,BC=BH=6,AH=AB-BH=4,在Rt△ADH中,由勾股定理得到 ,由此即可求出x的值.
【详解】解:由尺规作图痕迹可知,BD是∠ABC的角平分线,
过D点作DH⊥AB于H点,
∵∠C=∠DHB=90°,
∴DC=DH,
,
设DC=DH=x,则AD=AC-DC=8-x,BC=BH=6,AH=AB-BH=4,
在Rt△ADH中,由勾股定理:,
代入数据:,解得,故,
故选:A.
17.(2021•绥化市)已知在中,,.点为边上的动点,点为边上的动点,则线段的最小值是( )
A. B. C. D.
【答案】B
【解析】
【分析】作点F关于直线AB的对称点F’,如下图所示,此时EF+EB= EF’+EB,再由点到直线的距离垂线段长度最短求解即可.
【详解】解:作点F关于直线AB的对称点F’,连接AF’,如下图所示:
由对称性可知,EF=EF’,
此时EF+EB= EF’+EB,
由“点到直线的距离垂线段长度最小”可知,
当BF’⊥AF’时,EF+EB有最小值BF0,此时E位于上图中的E0位置,
由对称性知,∠CAF0=∠BAC=90°-75°=15°,
∴∠BAF0=30°,
由直角三角形中,30°所对直角边等于斜边的一半可知,
BF0=AB=,
故选:B.
18. (2021•辽宁省本溪市)如图,在中,,由图中的尺规作图痕迹得到的射线与交于点E,点F为的中点,连接,若,则的周长为( )
A. B. C. D. 4
【答案】C
【解析】
【分析】根据作图可知平分,,由三线合一,解,即可求得.
【详解】平分,,
,
点F为的中点
的周长为:
故选C.
二.填空题
1. (2021•湖北省黄冈市)在Rt△ABC中,∠C=90°,∠B=30°,适当长为半径画弧,分别交AC,F;再分别以点E,F为圆心EF的长为半径画弧,两弧交于点P,作射线AD交BC于点D,则BD与CD的数量关系为: BD=2CD .
【分析】证明AD=DB=2CD,可得结论.
【解答】解:∵∠C=90°,∠B=30°,
∴∠CAB=90°﹣30°=60°,
由作图可知AD平分∠CAB,
∴∠CAD=∠BAD=30°,
∴AD=2CD,
∵∠BAD=∠B=30°,
∴AD=DB,
∴BD=2CD,
故答案为:BD=2CD.
2. (2021•江苏省苏州市)如图,在Rt△ABC中,∠C = 90°.AF = EF.若∠CFE = 72°.则∠B = ▲ °.
【分析】根据等边对等角可得∠A=∠AEF,再根据∠A+∠AEF=∠CFE=72°,求出∠A的度数,最后根据在Rt△ABC中,∠C=90°,即可求出∠B的度数.
【解答】解:∵AF=EF,
∴∠A=∠AEF,
∵∠A+∠AEF=∠CFE=72°,
∴∠A=×72°=36°,
在Rt△ABC中,∠A=36°,
∴∠B=90°﹣36°=54°.
故答案为:54.
3. (2021•江苏省扬州) 如图,在中,,点D是的中点,过点D作,垂足为点E,连接,若,,则________.
【答案】3
【解析】
【分析】根据直角三角形的性质得到AB=10,利用勾股定理求出AC,再说明DE∥AC,得到,即可求出DE.
【详解】解:∵∠ACB=90°,点D为AB中点,
∴AB=2CD=10,
∵BC=8,
∴AC==6,
∵DE⊥BC,AC⊥BC,
∴DE∥AC,
∴,即,
∴DE=3,
故答案为:3.
4. (2021•湖南省娄底市)如图,中,是上任意一点,于点于点F,若,则________.
【答案】1
【解析】
【分析】将的面积拆成两个三角形面积之和,即可间接求出的值.
【详解】解:连接,如下图:
于点于点,
,
,
,
故答案是:1.
5. (2021•四川省成都市)如图,数字代表所在正方形的面积,则A所代表的正方形的面积为 100 .
【分析】三个正方形的边长正好构成直角三角形的三边,根据勾股定理得到字母A所代表的正方形的面积A=36+64=100.
【解答】解:由题意可知,直角三角形中,一条直角边的平方=36,一直角边的平方=64,
则斜边的平方=36+64=100.
故答案为100.
6. (2021•四川省眉山市)如图,△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于点M和点N,作直线MN,交AD于点E,则DE的长为 .
【分析】直接利用基本作图方法结合线段垂直平分线的性质、等腰三角形的性质、勾股定理分别得出DC,AD的长,即可得出DE的长.
【解答】解:如图所示:连接EC,
由作图方法可得:MN垂直平分AC,
则AE=EC,
∵AB=AC=5,BC=6,AD平分∠BAC交BC于点D,
∴BD=DC=3,AD⊥BC,
在Rt△ABD中,AD===4,
设DE=x,则AE=EC=4﹣x,
在Rt△EDC中,
DE2+DC2=EC2,
即x2+32=(4﹣x)2,
解得:x=,
故DE的长为.
故答案为:.
7. (2021•浙江省杭州)如图,在直角坐标系中,以点A(3,1),AC,AD(1,1),点C(1,3),点D(4,4)(5,2),则∠BAC = ∠DAE(填“>”、“=”、“<”中的一个).
【分析】在直角坐标系中构造直角三角形,根据三角形边之间的关系推出角之间的关系.
【解答】解:连接DE,
由上图可知AB═2,BC═2,
∴△ABC是等腰直角三角形,
∴∠BAC═45°,
又∵AE═==,
同理可得DE==,
AD==,
则在△ADE中,有AE2+DE2═AD7,
∴△ADE是等腰直角三角形,
∴∠DAE=45°,
∴∠BAC=∠DAE,
故答案为:=
8. (2021•浙江省绍兴市))如图,在△ABC中,AB=AC,∠ABC=70°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连结AP,则∠BAP的度数是 15°或75° .
【分析】根据等腰三角形的性质可以得到△ABC各内角的关系,然后根据题意,画出图形,利用分类讨论的方法求出∠BAP的度数即可.
【解答】解:如右图所示,
当点P在点B的左侧时,
∵AB=AC,∠ABC=70°,
∴∠ACB=ABC=70°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=180°﹣70°﹣70°=40°,
∵CA=CP1,
∴∠CAP1=∠CP6A===55°,
∴∠BAP1=∠CAP1﹣∠CAB=55°﹣40°=15°;
当点P在点C的右侧时,
∵AB=AC,∠ABC=70°,
∴∠ACB=ABC=70°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=180°﹣70°﹣70°=40°,
∵CA=CP4,
∴∠CAP2=∠CP1A===35°,
∴∠BAP2=∠CAP2﹣∠CAB=35°+40°=75°;
由上可得,∠BAP的度数是15°或75°,
故答案为:15°或75°.
9. (2021•江苏省盐城市)如图,在Rt△ABC中,CD为斜边AB上的中线,若CD=2,则AB= 4 .
【分析】根据直角三角形斜边上的中线性质得出CD=AB,代入求出答案即可.
【解答】解:∵∠ACB=90°,CD为△ABC斜边AB上的中线,
∴CD=AB,
∵CD=2,
∴AB=2CD=4,
故答案为:4.
10. (2021•齐齐哈尔市)若直角三角形其中两条边的长分别为3,4,则该直角三角形斜边上的高的长为________.
【答案】2.4或
【解析】
【分析】分两种情况:直角三角形的两直角边为3、4或直角三角形一条直角边为3,斜边为4,首先根据勾股定理即可求第三边的长度,再根据三角形的面积即可解题.
【详解】若直角三角形的两直角边为3、4,则斜边长为,
设直角三角形斜边上的高为h,
,
∴.
若直角三角形一条直角边为3,斜边为4,则另一条直角边为
设直角三角形斜边上的高为h,
,
∴.
故答案为:2.4或.
11. (2021•贵州省铜仁市)如图,将边长为1的正方形ABCD绕点顺时针旋转到的位置,则阴影部分的面积是______________;
【答案】
12. (2021•深圳)如图,已知,是角平分线且,作的垂直平分线交于点F,作,则周长为________.
【解答】(垂直平分线上的点到线段两端点距离相等)
∴
∵,是角平分线
∴
∵
∴,
∴
13. (2021•江苏省南京市) 如图,在四边形中,.设,则______(用含的代数式表示).
【答案】
【解析】
【分析】由等腰的性质可得:∠ADB=,∠BDC=,两角相加即可得到结论.
【详解】解:在△ABD中,AB=BD
∴∠A=∠ADB=
在△BCD中,BC=BD
∴∠C=∠BDC=
∵
∴
=
=
=
=
故答案为:.
14. (2021•广西贺州市)如图,一次函数与坐标轴分别交于,两点,点,分别是线段,上的点,且,,则点的标为________.
【答案】
【解析】
【分析】过P作PD⊥OC于D,先求出A,B 的坐标,得∠ABO=∠OAB=45°,再证明△PCB≌△OPA,从而求出BD=2,OD=4−2,进而即可求解.
【详解】如图所示,过P作PD⊥OC于D,
∵一次函数与坐标轴分别交于A,两点,
∴A(-4,0),B(0,4),即:OA=OB,
∴∠ABO=∠OAB=45°,
∴△BDP是等腰直角三角形,
∵∠PBC=∠CPO=∠OAP=45°,
∴∠PCB+∠BPC=135°=∠OPA+∠BPC,
∴∠PCB=∠OPA,
又∵PC=OP,
∴△PCB≌△OPA(AAS),
∴AO=BP=4,
∴Rt△BDP中,BD=PD=BP÷=2,
∴OD=OB−BD=4−2,
∴P(-2,4−2).
故答案是:P(-2,4−2).
三、解答题
1. (2021•江西省)如图,在△ABC中,∠A=40°,∠ABC=80°,BE平分∠ABC交AC于点E,ED⊥AB于点D,求证:AD=BD.
证明:∵BE平分∠ABC交AC于点E,
∴∠ABE=∠ABC=×80°=40°,
∵∠A=40°,
∴∠A=∠ABE,
∴△ABE为等腰三角形,
∵ED⊥AB,
∴AD=BD.
2. (2021•浙江省杭州)如图,在△ABC中,∠ABC的平分线BD交AC边于点D,∠C=45°.
(1)求证:AB=BD;
(2)若AE=3,求△ABC的面积.
【分析】(1)计算出∠ADB和∠BAC,利用等角对等边即可证明;
(2)利用锐角三角函数求出BC即可计算△ABC的面积.
【解答】(1)证明:∵BD平分∠ABC,∠ABC=60°,
∴∠DBC=∠ABC=30°,
∵∠ADB=∠DBC+∠C=75°,
∠BAC=180°﹣∠ABC﹣∠C=75°,
∴∠BAC=∠ADB,
∴AB=BD;
(2)解:由题意得,BE===3,
∴BC=3+,
∴S△ABC=BC×AE=.
3. (2021•长沙市)如图,在中,,垂足,,延长至,使得,连接.
(1)求证:;
(2)若,,求的周长和面积.
【答案】(1)证明见解析;(2)周长为,面积为22.
【分析】
(1)先根据垂直的定义可得,再根据三角形全等的判定定理与性质即可得证;
(2)先根据全等三角形的性质可得,从而可得,再利用勾股定理可得,从而可得,然后利用勾股定理可得,最后利用三角形的周长公式和面积公式即可得.
【详解】
(1)证明:,
,
在和中,,
,
;
(2),,
,
,
,
,
,
,
,
,
,
则的周长为,
的面积为.
2021全国中考真题分类汇编--三角形 特殊三角形(无答案): 这是一份2021全国中考真题分类汇编--三角形 特殊三角形(无答案),共11页。
2021年全国中考数学真题分类汇编:三角形(无答案): 这是一份2021年全国中考数学真题分类汇编:三角形(无答案),共17页。
2021年全国中考数学真题分类汇编:相似三角形(无答案): 这是一份2021年全国中考数学真题分类汇编:相似三角形(无答案),共12页。













