初中数学沪教版 (五四制)八年级上册19．2 证明举例课文配套课件ppt

这是一份初中数学沪教版 (五四制)八年级上册19．2 证明举例课文配套课件ppt，共16页。PPT课件主要包含了联结AD，联结BC，即∠B∠C，自主小结等内容，欢迎下载使用。

1、判定两个三角形全等的方法有哪些？
2、如果已知两个三角形全等，我们又可以 得到什么结论？
AAS、ASA、SAS、SSS
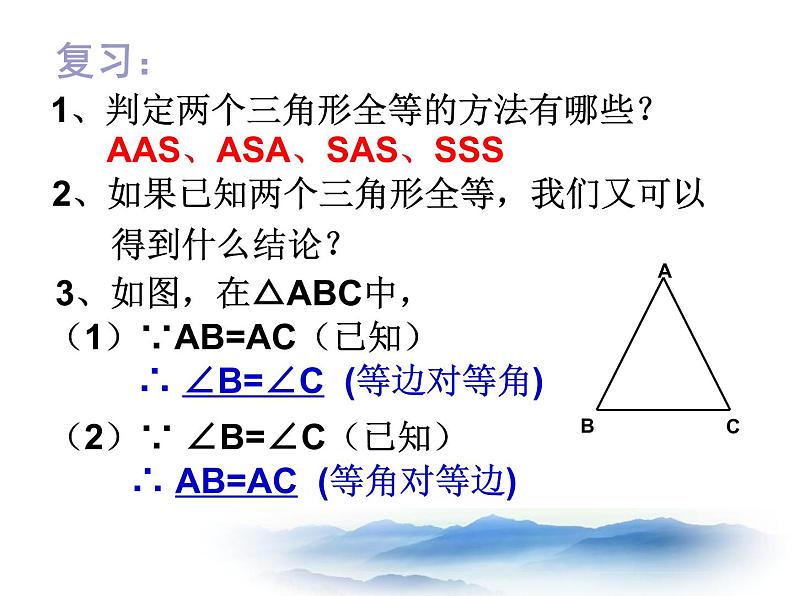
（1）∵AB=AC（已知）
∴ ∠B=∠C (等边对等角)
（2）∵ ∠B=∠C（已知）
∴ AB=AC (等角对等边)
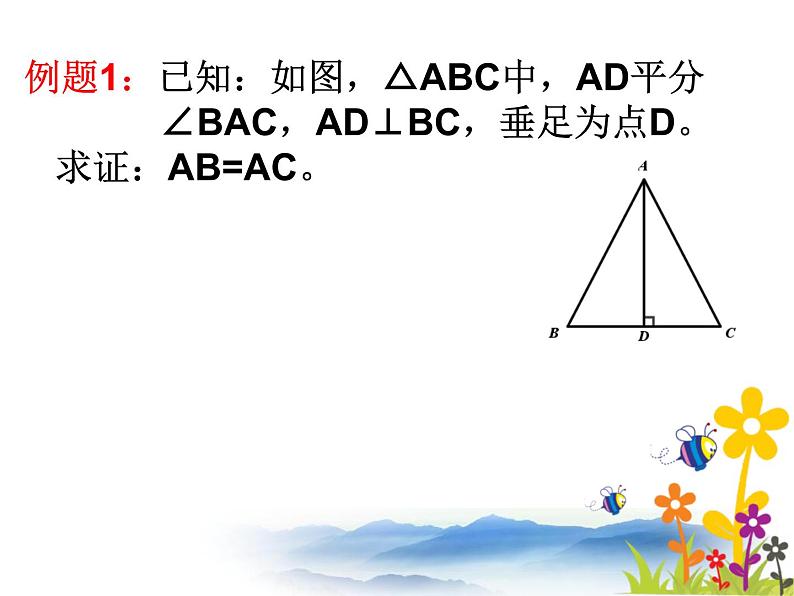
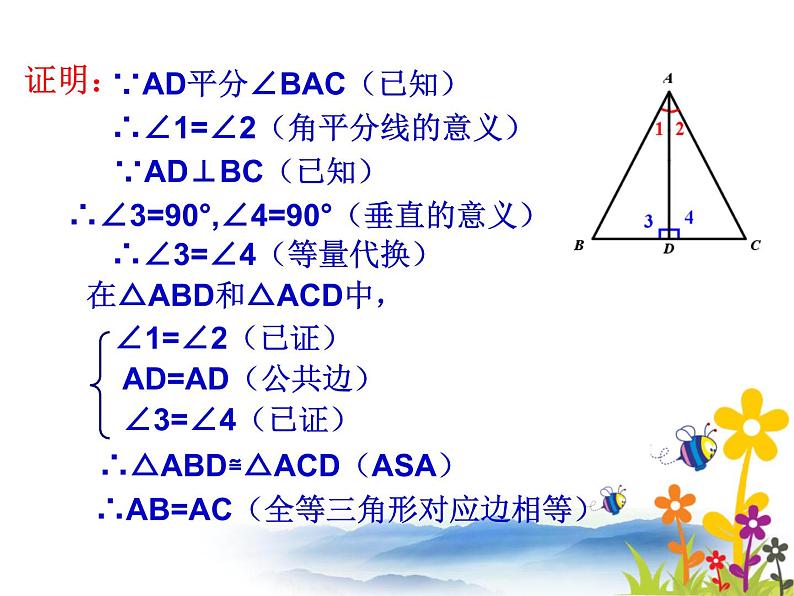
例题1：已知：如图，△ABC中，AD平分 ∠BAC，AD⊥BC，垂足为点D。 求证：AB=AC。
在△ABD和△ACD中，
∴△ABD≌△ACD（ASA）
∴AB=AC（全等三角形对应边相等）
∴∠B=∠C（等式性质）
∴AB=AC（等角对等边）
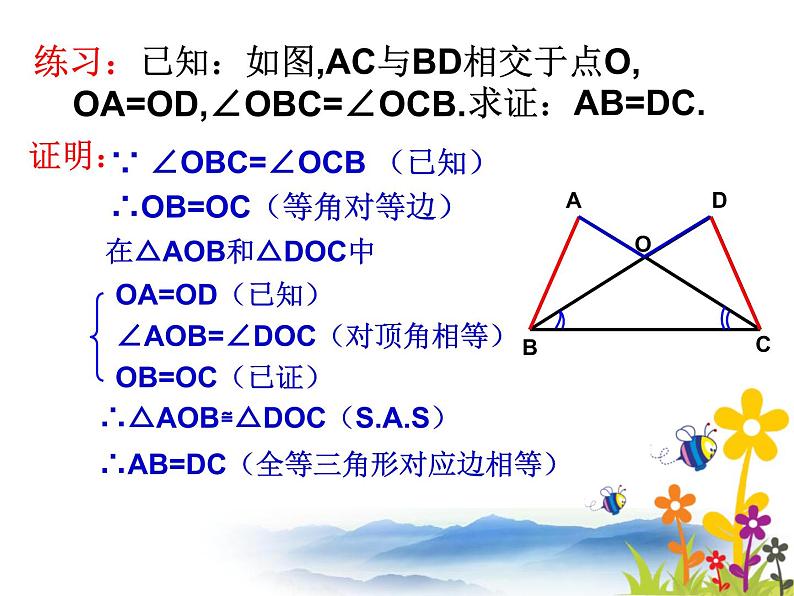
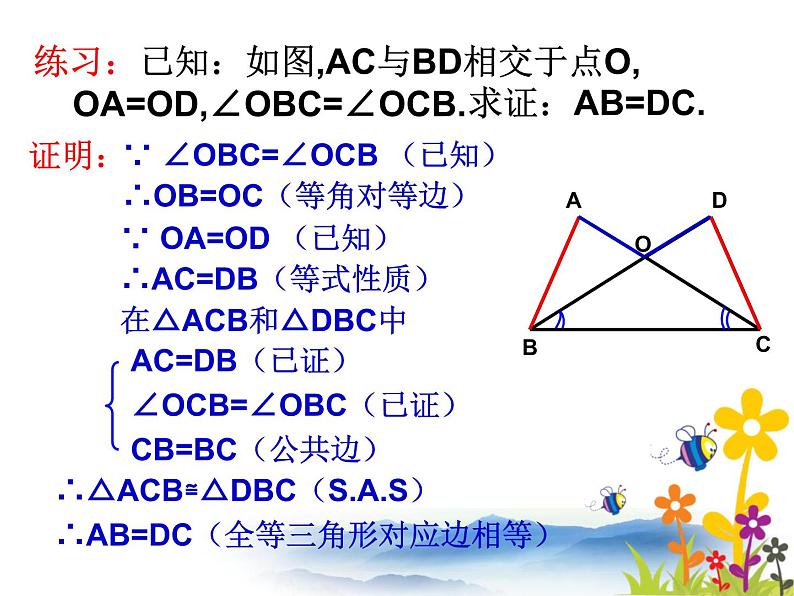
∵ ∠OBC=∠OCB （已知）∴OB=OC（等角对等边）
在△AOB和△DOC中
∴△AOB≌△DOC（S.A.S）∴AB=DC（全等三角形对应边相等）
在△ACB和△DBC中
∴△ACB≌△DBC（S.A.S）∴AB=DC（全等三角形对应边相等）
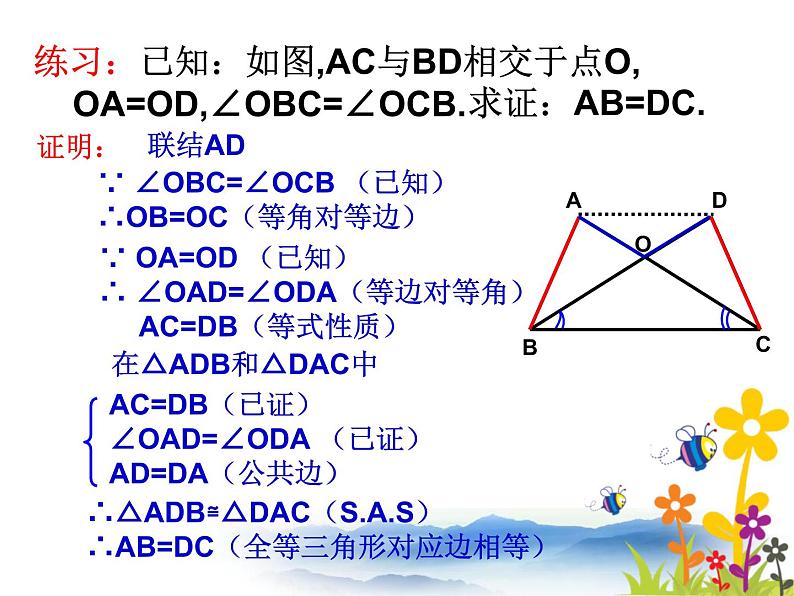
在△ADB和△DAC中
∴△ADB≌△DAC（S.A.S）∴AB=DC（全等三角形对应边相等）
∵ OA=OD （已知）∴ ∠OAD=∠ODA（等边对等角） AC=DB（等式性质）
例题2 已知：如图，AB=AC，DB=DC. 求证：∠B=∠C.
在△ABD和△ACD中
∴△ABD≌△ACD（S.S.S）
∴∠B= ∠C（全等三角形对应角相等）
同理， ∠3 = ∠4
∴ ∠1+ ∠3= ∠2+ ∠4 （等式性质）
练习: 已知：如图，AB=AC,AD=AE,AB、DC 相交于点M，AC、BE相交于点N, ∠DAB= ∠EAC, 求证:∠D= ∠E 。
练习：已知：如图，E，F是线段BC上的 两点，AB∥CD，AB=DC，CE=BF， 求证：AE＝DF。
练习 已知：如图，PB=PC，CE、BD 相交于点P，∠BDA=∠CEA. 求证：AB=AC.
这节课学习了哪些常用的方法证明两条线段相等、两个角相等？
此外还有哪些方法可以证明线段相等、角相等的？