人教版《24.1.3弧、弦、圆心角》同步练习含答案



24.1.3 弧、弦、圆心角同步练习

一、选择题

1.下列说法中，正确的是(    )

A.等弦所对的弧相等                           B.等弧所对的弦相等

C.圆心角相等，所对的弦相等                   D.弦相等所对的圆心角相等

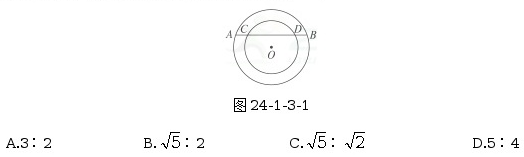
2.如图24-1-3-1，同心圆中，大圆的弦AB交小圆于C、D，已知AB=4，CD=2，AB的弦心距等于1，那么两个同心圆的半径之比为(    )

3.半径为R的⊙O中，弦AB=2R，弦CD=R，若两弦的弦心距分别为OE、OF，则OE∶OF等于(    )

A.2∶1                B.3∶2                 C.2∶3                 D.0

答案：C

二、填空题

1.．如图2,已知中,,且,则______.

2.．（2008襄樊市）如图3，⊙O中OA⊥BC，∠CDA=25°，则∠AOB的度数为           ．

答案.3.．如图，已知AB,CD是⊙O的直径，CE是弦，且AB∥CE,∠C=，则的度数为         

答案：

三、解答题（本题共2小题，每题10分，共20分）

4.．如图，AB是半圆O的直径，C、D是半径OA、OB的中点且OA⊥CE、OB⊥DE，求证==

证明：如图，连接OE、OF， ∵D是半径、OB的中点OB⊥DF，∴OD=5.．如图，在⊙中，，，ＯＣ分别交ＡＣ，ＢＤ于Ｅ、Ｆ，求证

9．如图所示，以ABCD的顶点A为圆心，AB为半径作圆，作AD，BC于E，F，延长BA交⊙O于G，求证：．

参考答案

一、选择题

  1．B  2．C   3. D   .

二、填空题

  4． 

5.50

  6．

三、解答题（本题共2小题，每题10分，共20分）

  7．证明：如图，连接OE、OF，

∵D是半径、OB的中点OB⊥DF，

∴OD=OF,∴∠OFD=,即∠FOD=，

同理∠EOA=,

∴∠FOD=∠EOA=∠EOF,

∴==

8．证明：如图，∵，∴,

∴,∵B,C是，

∴,

∴,∴

9．证明：连接AF，则AB=AF，所以∠ABF=∠AFB．

       因为四边形ABCD是平行四边形，所以AD∥BC，

所以∠DAF=∠AFB，∠GAE=∠ABF，所以∠GAE=∠EAF，所以．



第二十四章 圆

24.1 圆的有关性质

第三课时 弧、弦、圆心角

测试题

知识点1：圆心角及弧、弦、圆心角的关系

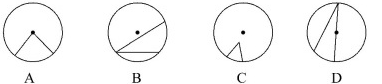
1.下列图形中表示的角是圆心角的是(　　)

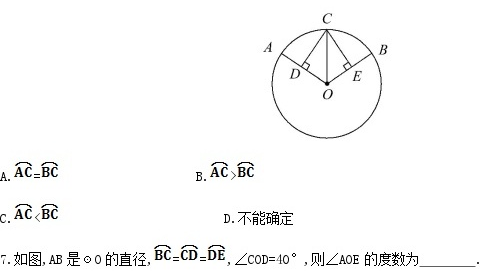
3.已知AB与A′B′分别是☉O与☉O′的两条弦,AB=A′B′,那么∠AOB与

∠A′O′B′的大小关系是(　　)

A.∠AOB=∠A′O′B′  B.∠AOB>∠A′O′B′

C.∠AOB<∠A′O′B′  D.不能确定

4.一条弦把圆分成1∶3两部分,则弦所对的圆心角为　　　　.

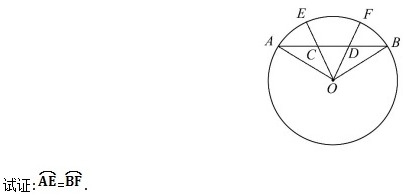
5.如图所示,AB是☉O的弦,C,D为弦AB上两点,且OC=OD,延长OC,OD,分别交☉O于点E,F.

知识点2：弧、弦、圆心角的应用

6.如图,D,E分别是☉O的半径OA, OB上的点,CD⊥OA,CE⊥OB,CD=CE,则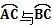与的关系是(　　)

(1)错因:                                             .

(2)纠错:____________________________________________________________

                                   .

【参考答案】

1.【解析】选A.根据圆心角的定义:顶点在圆心的角是圆心角可知,B,C,D项图形中的顶点都不在圆心上,所以它们都不是圆心角.

【易错提醒】若一个角的顶点不在圆心,这个角一定不是圆心角.

2. 【解析】选A.在同圆中,相等的圆心角所对的弧相等,可得选项A正确.

3. 【解析】选D.由弦相等推弦所对的圆心角相等,必须保证在同圆或等圆中.此题没有限制,所以不能确定∠AOB和∠A′O′B′的大小关系.

4.【解析】∵×360°=90°,∴弦所对的圆心角为90°.

答案:90°

5.【解题指南】1.证明两条弧相等,可证明这两条弧所对的圆心角相等.

2.常用等腰三角形的性质来求两个圆心角相等.

【证明】∵OC=OD,∴∠OCD=∠ODC.

∵AO=OB,∴∠A=∠B.

∴∠OCD-∠A=∠ODC-∠B,

即∠AOC=∠BOD,

即∠AOE=∠BOF.∴=.

6. 【解析】选A.∵CD⊥OA,CE⊥OB,

∴∠CDO=∠CEO=90°,

∵CD=CE,CO=CO,

∴△COD≌△COE,

∴∠COD=∠COE,

∴=.

【知识归纳】弧、弦、圆心角、弦心距的关系

1.圆心到弦的垂线段的长度叫弦心距.

2.在同圆或等圆中,如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中,有一组量相等,那么其余各组量都分别相等.

7.【解析】∵==,

∴∠BOC=∠DOE=∠COD=40°,

∴∠AOE=180°-3×40°=60°.

答案:60°

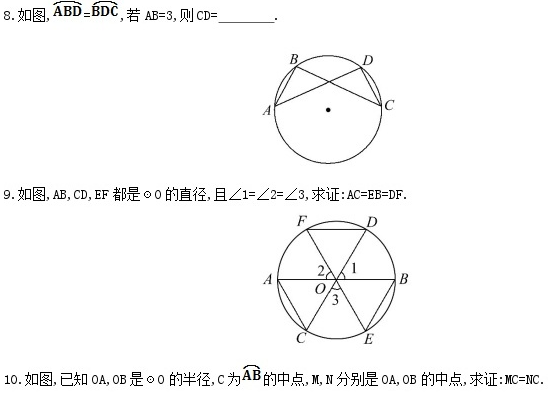
8.【解析】∵=,

∴-=-,即=,

∴CD=AB=3.

答案:3

9.【证明】在☉O中,∵∠1=∠2=∠3,

又∵AB,CD,EF都是☉O的直径,

∴∠FOD=∠AOC=∠BOE.

∴==,

∴AC=EB=DF.

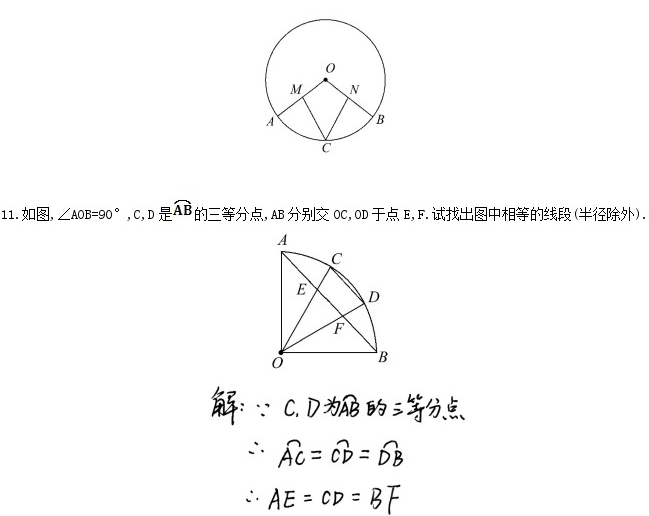
10.【证明】连接OC.

∵C为的中点,∴=,

∴∠MOC=∠NOC.

又∵M,N分别是OA,OB的中点,

∴OM=OA,ON=OB,

∴OM=ON.

又∵OC=OC,

∴△OMC≌△ONC,∴MC=NC.

【易错提醒】在同圆或等圆中,相等的圆心角或相等的弧所对的弦相等,不要认为所对的线段相等.

11. 【答案：】(1) AE,BF不是圆的弦,不能直接利用等弧对等弦.

(2)连接AC,BD，∵,∴AC=CD=BD.

易得出△ACE,△BDF,△OEF均为等腰三角形,∴AC=AE,BD=BF,

∴AE=CD=BF,OE=OF,CE=DF.时,点P到圆上一点的最长距离为4×2+2=10