新人教版《中心对称图形》(共两篇)

新人教版数学九年级上册第二十三章第二节中心对称图形课时练习
一、选择题
1.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
答案:C
知识点:中心对称及中心对称图形 多边形内角与外角 平行线的性质
解析:解答:A是假命题,因为如下图,△ADE与△ABC都是等腰三角形,但两个三角形并不全等;B是假命题,正多边形的每个内角为
,所以正多边形的每一个内角的度数随边数增多而变大;C是真命题,菱形的对称中心为两条对角线的交点,对称轴是两条对角线所在直线;D是假命题,两直线平行,同旁内角互补.
分析:对于错误命题的判定依据为举反例.
2.下列图形中不是轴对称而是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.矩形 D.菱形
答案:B
知识点:中心对称及中心对称图形 轴对称图形
解析:解答:等边三角形不是中心对称图形,对称轴为三条中线所在直线;平行四边形的对称中心为两条对角线的交点,不是轴对称图形;矩形的对称中心为两条对角线的交点,对称轴为两对边中点连线所在直线;菱形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线;所以选择B.
分析:根据中心对称图形与轴对称图形的定义解题.
3.下列图形中既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.等腰三角形
C.菱形 D.平行四边形
答案:C
知识点:中心对称及中心对称图形
解析:解答:等边三角形不是中心对称图形,对称轴为三条中线所在直线;等腰三角形不是中心对称图形,对称轴为底边上的中线所在直线;平行四边形的对称中心为两条对角线的交点,不是轴对称图形;菱形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线;所以选择C.
分析:根据中心对称图形与轴对称图形的定义解题.
4.下列图形中是轴对称而不是中心对称图形的是( )
A.平行四边形 B.线段
C.角 D.正方形
答案:C
知识点:中心对称及中心对称图形
解析:解答:平行四边形的对称中心为两条对角线的交点,不是轴对称图形;线段的对称中心为线段的中点,对称轴为线段的中垂线;角不是中心对称图形,对称轴为角平分线所在直线;正方形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线及两条对边中点连线所在直线;所以选择C.
分析:根据中心对称图形与轴对称图形的定义解题.
5.已知下列命题:
(1)关于中心对称的两个图形一定不全等;(2)关于中心对称的两个图形是全等形;(3)两个全等的图形一定关于中心对称;其中真命题的个数是( )
A.0 B.1 C.2 D.3
答案:B
知识点:中心对称及中心对称图形
解析:解答:关于中心对称的两个图形一定是全等形,所以(1)错误,(2)正确;(3)两个全等的图形位置可以是任意的,不一定是中心对称的,所以真命题只有一个.
分析:中心对称的两个图形一定全等,而两个全等的图形并不一定全等.
6.如图,不是中心对称图形的是( )
答案:B
知识点:中心对称及中心对称图形
解析:解答:中心对称的图形绕对称中心旋转180°后能与原来的图形重合,只有B项中的图形符合.
分析:根据中心对称图形定义解题.
7.△ABC和△关于点O对称,下列结论不正确的是( )
A.AO= B.AB∥
C.CO=BO D.∠BAC=∠
答案:C
知识点:中心对称及中心对称图形
解析:解答:点C与点B不是对称点,所以线段CO不一定与线段OB相等.
分析:两个图形中心对称,那么对称点所连线段都经过对称中心,而且被对称中心所平分.
8.下列说法中正确的是( )
A.能重合的图形一定是成轴对称图形
B.成中心对称的图形一定是重合的图形
C.两个成中心对称的图形的对称点连线不一定过对称中心
D.两个会重合的三角形一定关于某一点成中心对称
答案:B
知识点:中心对称及中心对称图形
解析:解答:轴对称图形是沿对称轴折叠重合的图形,而全等的图形即可重合,所以A错误;中心对称的图形全等即可重合,所以B正确;成中心对称的图形的对称点连线一定过对称中心,所以C错误;全等的三角形关于某一点旋转180°后可以重合,才是成中心对称的.
分析:中心对称的两个图形一定全等,而两个全等的图形并不一定全等.
9.平面图形的旋转一般情况下会改变图形的( )
A.位置 B.大小 C.形状 D.性质
答案:A
知识点:图形的旋转
解析:解答:旋转和平移一样只改变图形的位置.
分析:旋转一样只改变图形的位置,不改变图形的大小、形状与性质.
10.等边三角形与它本身重合,需绕着它的三边中线的交点旋转至少( )
A.60° B.180° C.360° D.120°
答案:D
知识点:旋转对称图形
解析:解答:如下图,△ABC为等边三角形,点O为三边中线的交点,那么∠EOG=∠GOF=∠EOF,所以△ABC旋转120°即可与本身重合.

分析:注意题中的至少,所以不可以选C.
11.下列命题中的真命题是( )
A.全等的两个图形是中心对称图形 B.关于中心对称的两个图形全等
C.中心对称图形都是轴对称图形 D.轴对称图形都是中心对称图形
答案:B
知识点:中心对称及中心对称图形 轴对称图形
解析:解答:中心对称的两个图形全等,但全等的两个图形不一定中心对称,所以A的说法错误,B的说法正确;中心对称图形与轴对称图形是两个不同的概念,没有必然的联系,所以C、D错误.
分析:判断一个图形是中心对称图形还是轴对称图形要根据定义.
12.下列图形中,既是轴对称图形又是中心对称图形的是( )
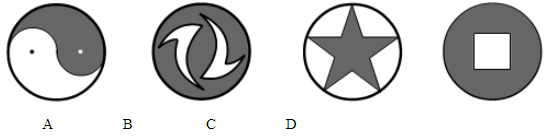
答案:D
知识点:中心对称及中心对称图形 轴对称图形
解析:解答:A中图形即不是轴对称图形,也不是中心对称图形;B中图形是中心对称图形,但不是中心对称图形;D中图形既是轴对称图形,又是中心对称图形.
分析:轴对称图形是沿某一直线对折可以重合的图形,中心对称图形是绕某一点旋转180°可以与自身重合的图形.
13.下列图形中,是轴对称图形但不是中心对称图形的是( )
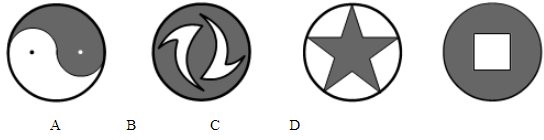
答案:C
知识点:中心对称及中心对称图形 轴对称图形
解析:解答:A中图形即不是轴对称图形,也不是中心对称图形;B中图形是中心对称图形,但不是中心对称图形;D中图形既是轴对称图形,又是中心对称图形.
分析:轴对称图形是沿某一直线对折可以重合的图形,中心对称图形是绕某一点旋转180°可以与自身重合的图形.
14.如图,四边形ABCD是正方形,△ADE绕着点A旋转90°后到达△ABF的位置,连接EF,则△AEF的形状是( )
A.等腰三角形 B.锐角三角形 C.等腰直角三角形 D.等边三角形
答案:C
知识点:图形的旋转
解析:解答:根据题意可知AF=AE,∠FAE为旋转角即∠FAE=90°,所以△AEF为等腰直角三角形.
分析:旋转的性质:对称点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角.
15.下列标志既是轴对称图形又是中心对称图形的是( )
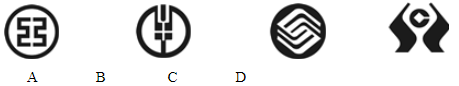
答案:A
知识点:中心对称及中心对称图形 轴对称图形
解析:解答:A既是轴对称图形,也是中心对称图形;B是轴对称图形,但不是中心对称图形;C中心对称图形,但不是轴对称图形.
分析:轴对称图形是沿某一直线对折可以重合的图形,中心对称图形是绕某一点旋转180°可以与自身重合的图形.
二、填空题:
1.关于中心对称的两个图形,对称点的连线经过 ,并被 平分.
答案:对称中心,对称中心
知识点:中心对称及中心对称图形
解析:解答:中心对称的性质.
分析:中心对称的性质.
2.关于中心对称的两个图形对应线段 .
答案:平行且相等
知识点:中心对称及中心对称图形
解析:解答:中心对称的性质.
分析:中心对称的性质.
3.线段、两相交直线、角、等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形、圆等图形中是中心对称图形的有: .
答案:线段、两条相交直线、平行四边形、矩形、菱形、正方形、圆
知识点:中心对称及中心对称图形
解析:解答:线段、两条相交直线、矩形、菱形、正方形、圆既是中心对称图形,也是轴对称图形;平行四边形是中心对称图形,但不是轴对称图形;角、等腰三角形、等边三角形是轴对称图形,不是中心对称图形.
分析:作出图形可以帮助解题.
4.关于点O成中心对称的两个四边形ABCD和HEFG,AD、BE、CF、DG都过 ;
并被点 所 ,AB∥ ,BC∥ , FG∥ .
答案:点O;O,平分,HE,EF,CD
知识点:中心对称及中心对称图形
解析:解答:中心对称的性质.
分析:中心对称的性质.
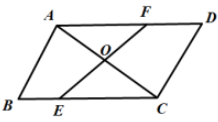
5.若点O是平行四边形ABCD对角线AC的中点,EF⊥AC于O交AD、BC分别于E、F,那么线段DE关于点O的对称线段是 .
答案:BF
知识点:中心对称及中心对称图形
解析:解答:根据题意可做如下图,可以看出点E关于点O的对称点为F,点D关于点O的对称点为B,所以线段DE关于点O的对称线段是BF.
分析:平形四边形是以对角线中点为对称中心的中心对称图形,找对称点时将该点绕点O旋转180°进行寻找.
三、解答题
1.已知点A的坐标为(,0),把点A绕着坐标原点顺时针旋转135º到点B,求点B的坐标.
答案:(-1,-1)
知识点:中心对称及中心对称图形
解析:解答:解:把A(,0)绕坐标原点顺时针旋转135°到点B,则点B在第三象限且与y轴夹角为45°,所以点B的坐标为(-1,-1).
分析:先根据旋转的方向与角度确定点B的位置.
2.如图,已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.
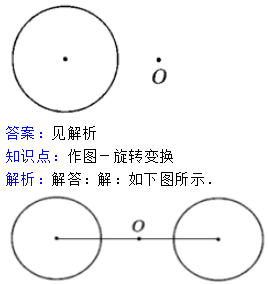
分析:先找到该圆关于点O中心对称的圆心,再以相等的半径作圆即可.
(练习)中心对称(第2课时)



