人教版《23.2.2中心对称图形》（含答案）共两篇



23.2.2　中心对称图形

基础题

知识点1　认识中心对称图形

1．(重庆中考)下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是(　　)

2．(哈尔滨中考)下列图形中，不是中心对称图形的是(　　)

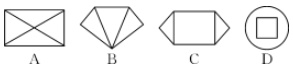
3．(郴州中考)下列图形既是轴对称图形又是中心对称图形的是(　　)

A．等腰三角形     B．平行四边形

C．矩形           D．等腰梯形

4．(黄石中考)在下列艺术字中既是轴对称图形又是中心对称图形的是(　　)

5．(南通中考)下列图形中既是轴对称图形又是中心对称图形的是(　　)

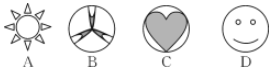
6．(莱芜中考)下列图形中，是轴对称图形，但不是中心对称图形的是(　　)

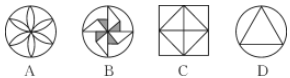
7．(山西中考)晋商大院的许多窗格图案蕴含着对称之美，现从中选取以下四种窗格图案，其中是中心对称图形但不是轴对称图形的是(　　)

8．(徐州中考)顺次连接正六边形的三个不相邻的顶点，得到如图所示的图形，该图形(　　)

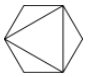
A．既是轴对称图形也是中心对称图形

B．是轴对称图形但并不是中心对称图形

C．是中心对称图形但并不是轴对称图形

D．既不是轴对称图形也不是中心对称图形

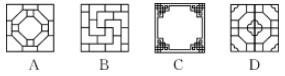
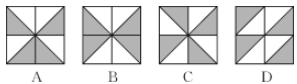
9．(三明中考)下列正方形中由阴影部分组成的图形，既是轴对称图形又是中心对称图形的是(　　)

知识点2　中心对称图形的性质

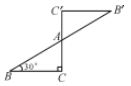
10．(东西湖区校级期末)如图是一个中心对称图形，A为对称中心，若∠C＝90°，∠B＝30°，BC＝2，则BB′的长为________．

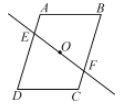
11．如图，直线EF经过ABCD的对角线的交点，若AE＝3 cm，四边形AEFB的面积为15 cm2，则CF＝________，四边形EDCF的面积为________．

12．如图是某种标志的一部分，其对称中心是点A.请补全图形．

中档题

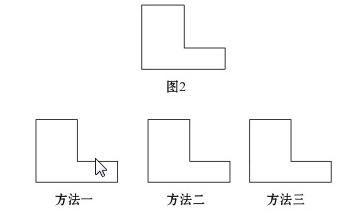
13．三张扑克牌如图1所示放在桌子上，小敏把其中一张旋转180°后得到如图2所示，则她所旋转的牌从左数起是(　　)

A．第一张      B．第二张

C．第三张      D．都不是

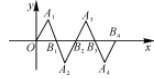
14．(庆阳中考)在如图所示的平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2A3B3与△B2A2B1关于点B2成中心对称，如此作下去，则△B2nA2n＋1B2n＋1(n是正整数)的顶点A2n＋1的坐标是(　　)

A．(4n－1，)      B．(2n－1，)

C．(4n＋1，)      D．(2n＋1，)

15．(宁波中考)如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为(　　)

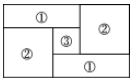
A．①②        B．②③

C．①③        D．①②③

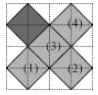
16．如图，在4×4的正方形网格中，每个小正方形的顶点称为格点，左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形)．再作一个格点正方形，并涂上阴影，使这两个格点正方形无重叠面积，且组成的图形是轴对称图形，又是中心对称图形．

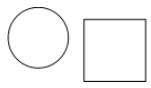
17．你能否画出一条直线，同时把如图所示的两个图形分成形状、大小都相同的两个部分？你还有什么发现？

综合题

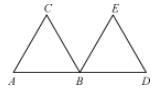
18．用六根一样长的小棒搭成如图所示的图形．

(1)试移动AC，BC这两根小棒，使六根小棒成为中心对称图形；

(2)若移动AC，DE这两根，能不能也达到要求呢？(画出图形)

参考答案

基础题

1．B　2.B　3.C　4.D　5.A　6.D　7.B　8.B　9.B　10.8　11.3 cm　15 cm2　12.图略．

中档题

13.A　14.C　15.A　

16.答案不唯一，如图(1)、(2)、(3)、(4)中任何一个位置都行．　17.直线既经过圆心又经过正方形对角线的交点．

综合题

18．(1)如图1：

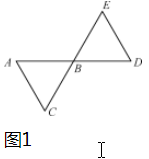
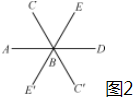
(2)能．如图2：



23.2.2中心对称图形一点就通

【知识回顾】

1.中心对称图形的概念

(1)如图1所示,把电风扇叶片绕着中心点H旋转180°,旋转后的图形_____(填“能”或“不能”)与原来的图形重合.

(2)如图2所示,把平行四边形绕着对角线的交点O旋转180°,旋转后的图形___填“能”或“不能”)与原来的图形重合,所以平行四边形是_________图形.

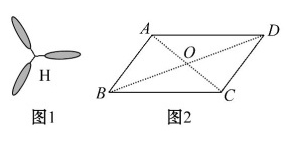
(3)把一个图形绕着某一点旋转______,如果旋转后的图形能够与原来的图形_____,那么这个图形叫做中心对称图形,该点就是_________.

2.中心对称图形的性质

如果一个图形是中心对称图形,那么_________是任意一对对应点连线的中点.

【夯实基础】

1、下列数字既是轴对称图形又是中心对称图形的有几个(   )

A.1个  B.2个  C.3个  D.4个

2、下列图形中,是轴对称图形但不是中心对称图形的是(    )

A.线段  B.等边三角形  C.正方形   D.圆

3、若两个图形关于某一点成中心对称，那么下列说法：（   ）.

①对称点的连线必过对称中心；    ②这两个图形一定全等；

③对应线段一定平行且相等；

④将一个图形绕对称中心旋转180°必定与另一个图形重合。其中正确的是

A.①②   B .①③ C.①②③  D.①②③④

4、下列说法中,错误的是(   )

A.中心对称就是中心对称图形

B.两个三角形关于某一点对称,则它们一定全等

C.直角是轴对称图形,但不是中心对称图形

D.中心对称图形是说明一个图形的形状特征

5、在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中，是轴对称图形的有______________,是中心对称图形的有____________,既是轴对称图形又是中心对称图形的有____________.

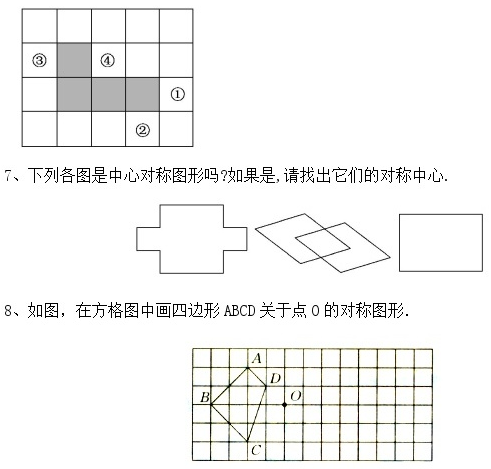
6、在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是     .

【提优特训】

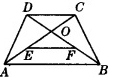
1、把等腰△ABC沿底边BC翻折,得到△DBC,那么四边形ABDC(    )

A.是中心对称图形,不是轴对称图形

B.是轴对称图形,不是中心对称图形

C.既是中心对称图形,又是轴对称图形

D.以上都不正确

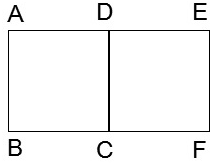
2、如图所示，等腰梯形ABCD中，AB∥CD，AB=2CD．AC，BD交于点O，且点E、F分别为OA、OB的中点，则下列关于点O成中心对称的一组三角形是（  ）    A．△ABO与△CDO;  B．△AOD与△BOC; C．△CDO与△EFO; D．△ACD与△BCD

3、如图，如果正方形CDEF旋转后能与正方形ABCD重合，那么图形所在的平面
上可以作为旋转中心的点共有（     ）。

A. 4       B. 3       C. 2        D.1

4、从数学对称的角度看,下面的几组大写英文字母(1)A N E G.(2)K B X M.(3)X I H O.(4)Z D W H,不同于另外三组的一组是    ;这一组英文字母的特点是    .

5、四边形ABCD中,对角线AC和BD相互平分,交点为O,则四边形ABCD的对称中心是      .

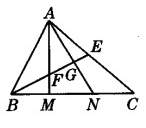
6、如图所示，△ABC中，M、N是边BC的三等分点，BE是AC边上的中线，连接AM、AN，分别交BE于F、G，求BF：FG：CE的值．

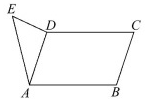
7、已知:如图,平行四边形ABCD及△ADE.

求作:点F,使多边形ABFCDE为中心对称图形,并说明理由.

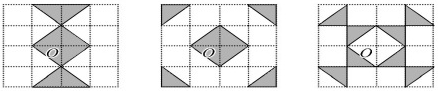
8、阅读材料:对于中心对称图形,过对称中心的任意一条直线都把这个图形的面积分成相等的两部分,如图

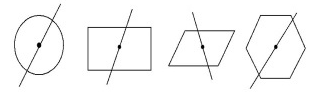
尝试应用:(1)将图1分成面积相等的两部分(不写作法,保留作图痕迹):

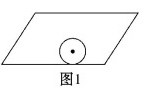
(2)用不同的方法把图2分成面积相等的两部分:

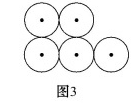
拓展延伸:把图3分成面积相等的两部分.

【中考链接】

1.（哈尔滨中考）下列图形中,既是轴对称图形又是中心对称图形的是(   )

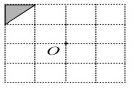
2.(荆州中考)如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.

【参考答案】

【夯实基础答案】

1. B  2. B   3. C    4.A  

5. ①②③④⑥⑦⑧⑨      ①⑤⑥⑦⑧⑨    ①⑥⑦⑧⑨

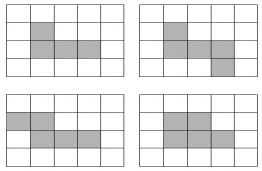
6.根据题意,可作出四种图形如下,其中旋转180°与自身重合的只有第2个图形,所以将②涂黑能构成中心对称图形.

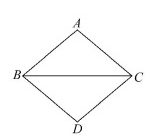
7.三种图形都是中心对称图形,它们的对称中心如图所示.

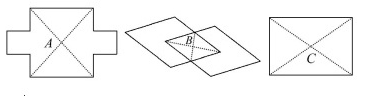
8.略

【提优特训答案】

1. C   2. C   3.B

1. (3)     既是中心对称图形又是轴对称图形

5.点O

6．解：如答图所示．

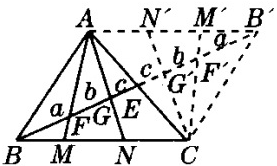
作已知图形的中心对称图形，以E为对称中心．令BF=a，FG=b，GE=c．

∵M′C∥AM，N′C∥AN

∴a：（2b+2c）=BM：MC=1：2

∴a=b+c，而（a+b）：2c=BN：NC=2：1

∴：a+b=4c，所以a=c，b=c．

∴BF：FG：GE=5：3：2．

点拨：要求线段的比，通过作平行线构造比例线段是一种重要的方法．

8.尝试应用(1)

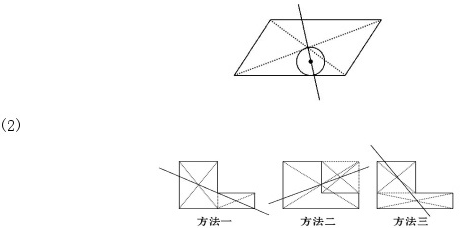
拓展延伸:

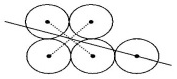
【中考链接答案】

1. D

2. 给左上角的三角形的面积为×1×1=,故设计图案总共需要三角形4÷=8(个),以O为对称中心的中心对称图形,同时又是轴对称图形的设计方案很多,答案不唯一,